P11182 [ROIR 2018] 分形 (Day2)
题目描述
**译自 ROI 2018 Regional. Day2 T3.** ***[Красота фейерверка](http://neerc.ifmo.ru/school/archive/2017-2018/ru-olymp-regional-2018-day2.pdf)***
已知一棵包含 $n$ 个元素的有根树 $T^1$。定义 $T^m$ 为一棵树,生成方式是在 $T^{m-1}$ 的每个叶结点下面连一棵 $T^1$ 而得。
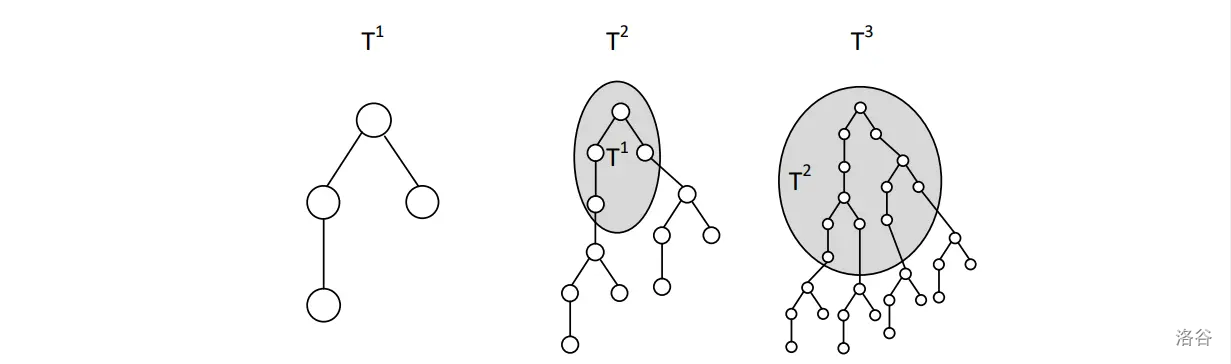
试求 $T^m$ 的直径的长度(这里的长度指的是直径上的点数)。
输入格式
第一行 $n,m$。
第二行 $p_2\ldots p_n,\ \ $ $p_i$ 表示结点 $p_i$ 与结点 $i$ 有边连接。
输出格式
输出一行一个整数,表示答案。
说明/提示
### 样例解释
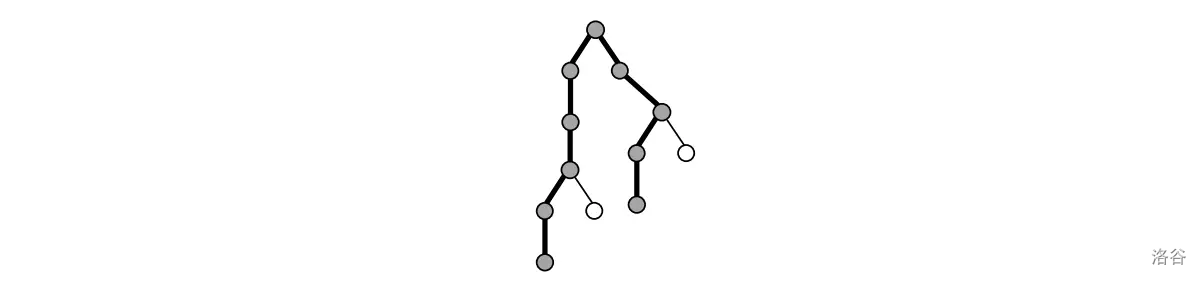
### 数据范围
$3≤n≤2\times 10^5,$ $1≤m≤2\times 10^5,$ $1\le p_i\le i-1.$
|子任务编号|分值|$n$|$m$|
|:-:|:-:|:-:|:-:|
|1|19|$3 ≤ n ≤ 5000$|$m = 1$|
|2|10| |$m=1$|
|3|20|$3 ≤ n ≤ 5000$|$1 ≤ m ≤ 5000$|
|4|19|$3 ≤ n≤ 5000$||
|5|32|| |