「KDOI-10」超级演出

[English Statement](https://www.luogu.com.cn/problem/T519360). You must submit your code at the Chinese version of the statement. **本场比赛所有题目从标准输入读入数据，输出到标准输出。**

巡准备了一场超级演出。舞台和候场室可以看作一个包含 $n$ 个点 $m$ 条边的有向图，并且这个图当中没有环，也就是说，这是一张有向无环图（DAG）。 舞台为 $1$ 号节点，**保证所有节点均有到达节点 $\bm 1$ 的路径**。其余的节点均为候场室，每个候场室恰有一个剧团进行等待。 巡可以对一个候场室 $u$ 发布出场命令： - 如果这个候场室的剧团还没有出场，并且存在一条 $u\to 1$ 的路径上没有其余候场的剧团。那么这个剧团就会沿着这条路径到达舞台进行演出，随后退场。注意：**一个剧团退场后不会重新回到候场室。** - 否则，这个命令被认为是无效的。 巡有一个命令序列 $a_1,a_2,\dots,a_k$ 和 $q$ 次询问，每次给出一个区间 $[l,r]$。巡想要知道如果依次对候场室 $a_l,a_{l+1},\dots,a_r$ 发布出场命令后，候场室还会剩下多少剧团等待演出。 注意：每次询问相互独立，也就是说，每次询问之前，每个候场室都恰有一个剧团进行等待。

从标准输入读入数据。 输入的第一行包含一个正整数 $c$，表示测试点编号。$c=0$ 表示该测试点为样例。 第二行包含四个正整数 $n,m,k,q$，表示图的点数，边数，序列长度，和询问次数。 接下来 $m$ 行，每行两个正整数 $u,v$，表示一条从 $u$ 到 $v$ 的有向边。保证无自环，无重边。 接下来的一行，$k$ 个正整数 $a_1,a_2,\dots,a_k$。 接下来 $q$ 行，每行两个正整数 $l,r$，表示一次询问的区间。

输出到标准输出。 $q$ 行，每行一个非负整数，表示一次询问的答案。

0
5 5 5 4
2 1
3 1
5 1
4 2
4 3
2 4 4 3 5
1 2
1 5
3 5
2 3

2
0
2
4

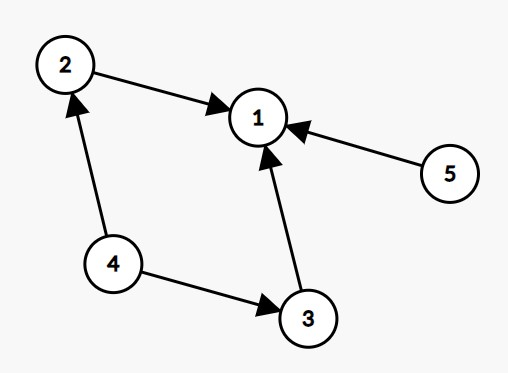
**【样例 1 解释】**  如图： - 当询问 $l=1,r=2$ 时： - 发布出场命令 $a_1=2$。$2$ 沿着 $2\to 1$ 出场。 - 发布出场命令 $a_2=4$。$4$ 沿着 $4\to 2\to 1$ 出场。 此时余下 $3,5$ 两个剧团，输出 $2$。 - 当询问 $l=2,r=3$ 时： - 发布出场命令 $a_2=4$。找不到 $4\to 1$ 的且路上没有别的剧团的路线，该指令被认为无效。 - 发布出场命令 $a_3=4$。找不到 $4\to 1$ 的且路上没有别的剧团的路线，该指令被认为无效。 此时余下 $2,3,4,5$ 四个剧团，输出 $4$。 **【样例 2】** 见选手目录下的 `show/show2.in` 与 `show/show2.ans`。 这个样例满足测试点 $1,2$ 的限制条件。 **【样例 3】** 见选手目录下的 `show/show3.in` 与 `show/show3.ans`。 这个样例满足测试点 $5\sim 8$ 的限制条件。 **【样例 4】** 见选手目录下的 `show/show4.in` 与 `show/show4.ans`。 这个样例满足测试点 $9\sim 11$ 的限制条件。 **【样例 5】** 见选手目录下的 `show/show5.in` 与 `show/show5.ans`。 这个样例满足测试点 $12,13$ 的限制条件。 **【样例 6】** 见选手目录下的 `show/show6.in` 与 `show/show6.ans`。 这个样例满足测试点 $18,19$ 的限制条件。 *** **【数据范围】** 对于全部的测试数据，保证： - $1\leq n,k,q\leq2\times10^5$； - $1\leq m\leq4\times10^5$； - $1\leq v<u\leq n$，且不存在两组相同的 $(u,v)$； - 对于任意 $1\le i\le k$，$2\leq a_i\leq n$； - 对于每组询问，$1\leq l\leq r\leq k$； - 输入构成一张有向无环图，且所有节点均存在到达节点 $1$ 的路径。 | 测试点 | $n,k,q\leq$ | $m\leq$ | 特殊性质 | |:--:|:--:|:--:|:--:| | $1,2$ | $300$ | $600$ | 无 | | $3,4$ | $2\,000$ | $4\,000$ | A | | $5\sim 8$ | $2\,000$ | $4\,000$ | 无 | | $9\sim 11$ | $2\times10^5$ | $4\times10^5$ | A | | $12,13$ | $2\times10^5$ | $4\times10^5$ | BC | | $14,15$ | $2\times10^5$ | $4\times10^5$ | C | | $16,17$ | $2\times10^5$ | $4\times10^5$ | BD | | $18,19$ | $2\times10^5$ | $4\times10^5$ | D | | $20\sim 22$ | $2\times10^5$ | $4\times10^5$ | B | | $23\sim 25$ | $2\times10^5$ | $4\times10^5$ | 无 | - 特殊性质 A：图退化为一棵内向树，也就是说，除节点 $1$ 外，每个点恰有一条出边，节点 $1$ 没有出边； - 特殊性质 B：保证对于每组询问，$r=k$； - 特殊性质 C：保证对于任意 $1\leq i< j\leq k$，$a_i\neq a_j$； - 特殊性质 D：保证每个点的入度和出度均不超过 $30$。