P11191 「KDOI-10」Super Show

|Input|Output|Time Limit|Memory Limit| |:--:|:--:|:--:|:--:| |standard input|standard output|1.0 s|512 MiB| This problem has $25$ tests. The full score is $100$ points, and $4$ points per test.

Meguru has prepared a super show! The stage and the waiting rooms can be seen as a directed acyclic graph (DAG) consisting of $n$ vertices and $m$ edges. The stage is at vertex $1$, and the rest vertices are all waiting rooms. It is guaranteed that each vertex has at least one path to vertex $1$. For each waiting room, there is a troupe in it initially. Meguru can send an *enter* command to a waiting room $u$: - If the troupe in this room has not come to the stage yet, and there exists a path from $u$ to $1$ such that there are no troupe waiting for entrance, then the troupe in waiting room $u$ will come to the stage and subsequently exit. Note that a troupe will **not** return to the waiting room after the exit. - Otherwise, this command is considered as *inoperative*. Meguru has a command sequence $a_1,a_2,\ldots, a_k$ and $q$ queries. In each query, an interval $[l,r]$ is given, and Meguru asks you that, if she sends the enter command to waiting room $a_l,a_{l+1},\ldots,a_r$ successively, how many troupes are still in the waiting room. Note that each query is **independent**, i.e., before each query, there is a troupe in each waiting room.

The first line of the input contains a single integer $c$ — the id of the test. $c=0$ represents that this is a sample test. The second line contains four integers $n$, $m$, $k$, and $q$ — the number of vertices, the number of edges, the length of the command sequence, and the number of queries. Then $m$ lines follow, each containing two integer $u$ and $v$ — there is an edge connecting $u$ and $v$. It is guaranteed that there are no self-loops or multiple-edges. The next line contains $k$ integers $a_1,a_2,\ldots, a_k$ — the command sequence. Then $q$ lines follow, each containing two integers $l$ and $r$ — the interval in the query.

Print $q$ lines, each line containing a single integer — the answer to the query.

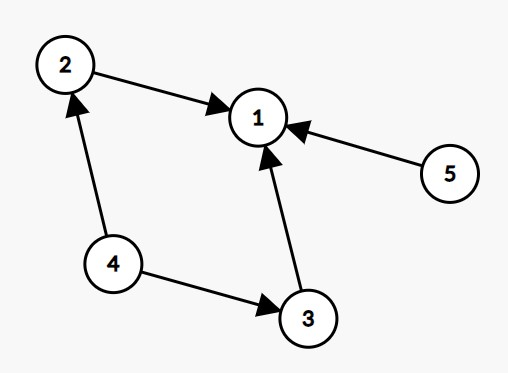
**Sample 1 Explanation**  - In the query $l=1$, $r=2$: - For the command $a_1=2$, $2$ comes to the stage by $2\to 1$; - For the command $a_2=4$, $4$ comes to the stage by $4\to 2\to 1$. Troupes $3,5$ are left, so output $2$. - In the query $l=2$, $r=3$: - For the command $a_2=4$, there does not exist a valid path, so this command is inoperative. - For the command $a_3=4$, there does not exist a valid path, so this command is inoperative. Troupes $2,3,4,5$ are left, so output $4$. **Sample 2** See `show/show2.in` and `show/show2.ans` in the attachments. This sample satisfies the constraints of test $1,2$. **Sample 3** See `show/show3.in` and `show/show3.ans` in the attachments. This sample satisfies the constraints of test $5\sim 8$. **Sample 4** See `show/show4.in` and `show/show4.ans` in the attachments. This sample satisfies the constraints of test $9\sim 11$. **Sample 5** See `show/show5.in` and `show/show5.ans` in the attachments. This sample satisfies the constraints of test $12,13$. **Sample 6** See `show/show6.in` and `show/show6.ans` in the attachments. This sample satisfies the constraints of test $18,19$. *** **Constraints** For all the tests, it is guaranteed that: - $1\leq n,k,q\leq2\times10^5$; - $1\leq m\leq4\times10^5$; - $1\leq v