【MX-J8-T2】黑洞

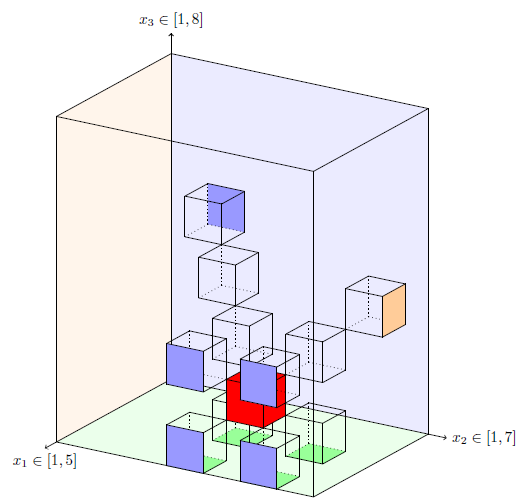
原题链接：<https://oier.team/problems/82>。 ---  上图给出了二维下与红点在同一条对角线上的所有方格。 考虑三维下的情况，下图给出了与红色方块在同一条对角线上的所有方块。  本题我们将会把对角线这个概念推广到 $n$ 维上。

已知一片 $n$ 维空间，第 $i$ 维的大小为 $m_i$。我们使用一个 $n$ 维坐标 $(x_1, x_2, \dots, x_n)$ 表示这片 $n$ 维空间里的一个位置，其中 $x_i$ 为 $[1, m_i]$ 间的整数。 在位置 $(a_1, a_2, \dots, a_n)$ 处有一颗黑洞。这片 $n$ 维空间中所有与它在同一条对角线上的位置都将被吞噬： - 称位置 $(a_1, a_2, \dots, a_n)$ 与 $(b_1, b_2, \dots, b_n)$ 在同一条对角线上，当且仅当存在一个整数 $k \geq 0$，使得对每个 $1 \leq i \leq n$，都有 $\lvert a_i - b_i \rvert = k$。 你需要求出共有多少个位置会被黑洞吞噬（即与黑洞在同一条对角线上，包括黑洞所处位置本身）。答案对 $10^9 + 7$ 取模。

第一行，一个正整数 $n$，表示维度数。 第二行，$n$ 个正整数 $m_1, \dots, m_n$，表示每一维的大小。 第三行，$n$ 个正整数 $a_1, \dots, a_n$，表示黑洞的位置。

仅一行一个整数，表示该 $n$ 维空间中被黑洞吞噬的位置个数。答案对 $10^9 + 7$ 取模。

2
6 6 
2 3

8

2
999999999 999999999
500000000 500000000

999999990

3
5 7 8
4 5 2

12

**【样例解释 \#1】** 如题目背景中的图所示，其中红色圆形为黑洞所在位置，黑色方格为被黑洞吞噬的位置，共 $8$ 个。 **【样例解释 \#2】** 有 $1999999997$ 个位置被黑洞吞噬，$1999999997$ 对 $10^9+7$ 取模的结果为 $999999990$。 **【样例解释 \#3】** 如题目背景中的图所示，$(1,2,5)$，$(2,3,4)$，$(2,7,4)$，$(3,4,1)$，$(3,4,3)$，$(3,6,1)$，$(3,6,3)$，$(4,5,2)$，$(5,4,1)$，$(5,4,3)$，$(5,6,1)$，$(5,6,3)$ 共 $12$ 个位置被黑洞吞噬。 **【样例 \#4】** 见附件中的 `hole/hole4.in` 与 `hole/hole4.ans`。 该组样例满足测试点 $9 \sim 10$ 的约束条件。 **【样例 \#5】** 见附件中的 `hole/hole5.in` 与 `hole/hole5.ans`。 该组样例满足测试点 $11 \sim 13$ 的约束条件。 **【样例 \#6】** 见附件中的 `hole/hole6.in` 与 `hole/hole6.ans`。 该组样例满足测试点 $14 \sim 19$ 的约束条件。 **【样例 \#7】** 见附件中的 `hole/hole7.in` 与 `hole/hole7.ans`。 该组样例满足测试点 $20 \sim 25$ 的约束条件。 **【数据范围】** 本题共 $25$ 个测试点，每个 $4$ 分。 |测试点编号|$n$|$m_i\le$| | :-----------: | :-------------:|:-----------:| |$1\sim2$|$=2$|$10^6$| |$3\sim4$|$=2$|$10^9$| |$5\sim6$|$=3$|$10^6$| |$7\sim8$|$=3$|$10^9$| |$9\sim10$|$\le20$|$15$| |$11\sim13$|$\le20$|$10^9$| |$14\sim19$|$\le1000$|$10^9$| |$20\sim25$|$\le2\times10^5$|$10^9$| 对于全部数据，保证：$2\le n\le 2\times10^5$，$1\le a_i\le m_i\le 10^9$。