P11229 [CSP-J 2024] 小木棍
题目描述
小 S 喜欢收集小木棍。在收集了 $n$ 根长度相等的小木棍之后,他闲来无事,便用它们拼起了数字。用小木棍拼每种数字的方法如下图所示。
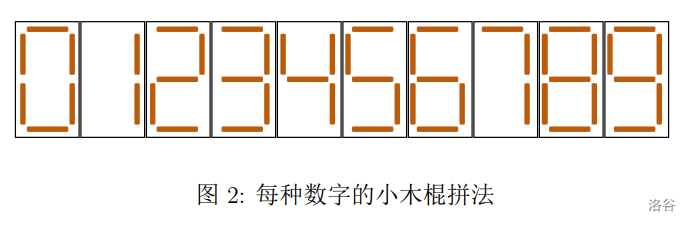
现在小 S 希望拼出一个**正**整数,满足如下条件:
- 拼出这个数**恰好**使用 $n$ 根小木棍;
- 拼出的数没有前导 $0$;
- 在满足以上两个条件的前提下,这个数尽可能小。
小 S 想知道这个数是多少,可 $n$ 很大,把木棍整理清楚就把小 S 折腾坏了,所以你需要帮他解决这个问题。如果不存在正整数满足以上条件,你需要输出 $-1$ 进行报告。
输入格式
本题有多组测试数据。
输入的第一行包含一个正整数 $T$,表示数据组数。
接下来包含 $T$ 组数据,每组数据的格式如下:
一行包含一个整数 $n$,表示木棍数。
输出格式
对于每组数据:输出一行,如果存在满足题意的正整数,输出这个数;否则输出 $-1$。
说明/提示
**【样例 1 解释】**
- 对于第一组测试数据,不存在任何一个正整数可以使用恰好一根小木棍摆出,故输出 $-1$。
- 对于第四组测试数据,注意 $0$ 并不是一个满足要求的方案。摆出 $9$、$41$ 以及 $111$ 都恰好需要 $6$ 根小木棍,但它们不是摆出的数最小的方案。
- 对于第五组测试数据,摆出 $208$ 需要 $5 + 6 + 7 = 18$ 根小木棍。可以证明摆出任何一个小于 $208$ 的正整数需要的小木棍数都不是 $18$。注意尽管拼出 $006$ 也需要 $18$ 根小木棍,但因为这个数有前导零,因此并不是一个满足要求的方案。
**【数据范围】**
对于所有测试数据,保证:$1 \leq T \leq 50$,$1 \leq n \leq 10^5$。
::cute-table{tuack}
| 测试点编号 | $n\leq$ | 特殊性质 |
| :----------: | :----------: | :----------: |
| $1$ | $20$ | 无 |
| $2$ | $50$ | ^ |
| $3$ | $10^3$ | A |
| $4,5$ | $10^5$ | ^ |
| $6$ | $10^3$ | B |
| $7,8$ | $10^5$ | ^ |
| $9$ | $10^3$ | 无 |
| $10$ | $10^5$ | ^ |
特殊性质 A:保证 $n$ 是 $7$ 的倍数且 $n \geq 100$。
特殊性质 B:保证存在整数 $k$ 使得 $n = 7k + 1$,且 $n \geq 100$。