P11263 [COTS 2018] 仲裁 Arbitraža
题目背景
译自 [Izborne Pripreme 2018 (Croatian IOI/CEOI Team Selection)](https://hsin.hr/pripreme2018/) D2T1。$\texttt{10s,1G}$。
题目描述
A 国和 B 国正在划分一块 $n\times m$ 的矩形土地。
显然,这块土地上有 $(n-1)$ 条水平线和 $(m-1)$ 条垂直线。
给这 $(n+m-2)$ 条线分配 $[1,k]$ 间的整数。定义一个格子的**权值**为在它左/上方的线上整数之和减去在它右/下方的线上整数之和。
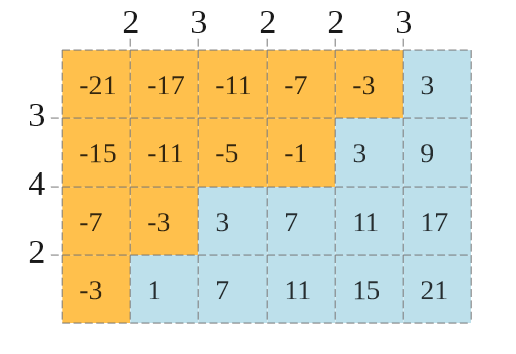
给定每个格子权值的要求(要求这个格子的权值 $\lt 0$ 或者 $\gt 0$)。在 $k^{n+m-2}$ 种分配整数的方案中,求出有多少个方案符合要求。
只需要输出答案对 $(10^9+7)$ 取模后得到的结果。
输入格式
第一行,三个正整数 $n,m,k$。
接下来一个 $n\times m$ 的矩阵,里面的元素不是 $\texttt{+}$ 就是 $\texttt{-}$,表示每个格子权值符号的要求。
输出格式
输出一行一个整数,表示答案。
说明/提示
对于 $100\%$ 的数据,保证 $1\le n,m,k\le 80$。
| 子任务编号 | $n$ | $m $ | $k\le$ | 特殊性质 | 得分 |
| :--: | :--: | :--: | :--: | :--: | :--: |
| $ 1 $ | $ \le 10 $ | $\le 10$ | $ 4$ | | $ 10 $ | |
| $ 2 $ | $ \le 80 $ | $=1$ | $80$ | | $ 10 $ |
| $ 3 $ | $\le20$ | $\le 20$ | $20$ | | $ 10 $ |
| $ 4 $ | $\le40$ | $\le 40$ | $40$ | |$ 20 $ |
| $ 5 $ | $\le79$ | $=n+1$ | $80$ | A |$ 20 $ |
| $ 6 $ | $\le 80$ | $\le 80$ | $80$ | |$ 30 $ |
特殊性质 A:$(i,j)$ 要求为 $\texttt{+}$,当且仅当 $i+j\ge m+1$。