P11264 [COTS 2018] 逃遁 Bijeg

译自 [Izborne Pripreme 2018 (Croatian IOI/CEOI Team Selection)](https://hsin.hr/pripreme2018/) D2T2。$\texttt{10s,1G}$。

考虑一个二维笛卡尔坐标系。 劫匪初始时在原点，此外有 $n$ 个警察分布在平面上。 他们的**速率**均为 $v$（一个正实数），且只会沿着一个特定的方向做**匀速直线**运动（每个人运动的方向可能不同）。 劫匪可以任意选定自己逃跑的方向，而警察会选择最优的方式追捕劫匪。当警察和劫匪的位置重合时，劫匪即被逮捕。 试判断： - 劫匪是否可以成功逃跑，也就是，是否存在一个方向，使得劫匪不被逮捕。 如果无法逃跑，还需要求出劫匪被逮捕时，离原点的欧几里得距离的最大值。 数据保证这 $(n+1)$ 个人的位置两两不同。

第一行，一个正整数 $n$。 接下来 $n$ 行，每行两个整数 $x,y$，描述警察的位置。 数据保证 $(n+1)$ 个人的位置两两不同。

如果劫匪可以成功逃跑，输出 $-1$。 否则，输出一个实数，表示劫匪被逮捕时距离的最大值。 当且仅当你的答案与标准答案的绝对或相对误差不大于 $10^{-5}$ 时，认为你的答案正确。

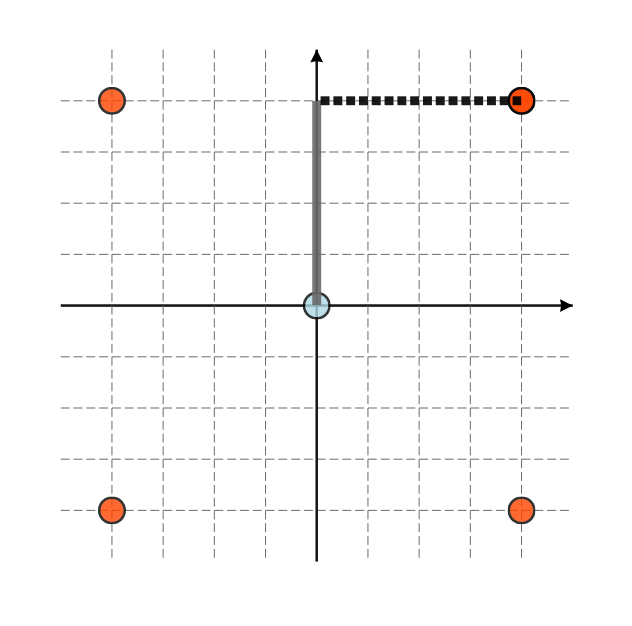
#### 样例解释 样例 $1$ 解释如图所示。  #### 子任务 对于 $100\%$ 的数据，保证 $1\le n\le 10^5$，$|x|,|y|\le 10^3$，所有人的位置均不同。 | 子任务编号 | $n\le $ | $\vert x\vert ,\vert y\vert \le $ | 得分 | | :--: | :--: | :--: | :--: | | $ 1 $ | $ 100 $ | $10$ | $ 20 $ | | $ 2 $ | $ 3\, 000 $ | $100$ | $ 30 $ | | $ 3 $ | $ 10^5$ | $1\, 000$ | $ 50 $ |