P11298 [NOISG 2018 Prelim] Island

翻译自 [NOISG 2018 Prelim C. Island](https://github.com/noisg/sg_noi_archive/tree/master/2018_prelim)。 **本题已启用 Special Judge，满足题目条件的任何答案都将视为正确。保证 SPJ 用时不超过 $1$ 秒**。

老鼠吱吱发现了一座小岛，这座小岛上的人以捕鱼为生，所以他们的 $n$ 所房子（标号为 $1$ 到 $n$）都在小岛的**边缘**，大家还需要交换各自的鱼，所以有些路在小岛的中间。 为了连接城镇，在岛的内部创建了 $m$ 个路口（标号为 $n+1$ 到 $n+m$）。为了最大限度地降低建设成本，这个岛上**只有 $n+m−1$ 条路**，这样任何两个城镇之间就有且仅有一条路。 换言之，道路网络可以**表示为一棵树**，有 $n$ 个叶子（代表 $n$ 所房子）和 $m$ 个非叶子节点（代表 $m$ 个路口）。根据树的性质，这棵树有 $n+m−1$条边（代表 $n+m-1$ 条路）。 此外，**每个路口至少有三条路与之相连**，除了路口外，路不会与其他路相交，也没有桥梁或隧道（它们很贵）。以下是一个有 $37$ 所房子、$20$ 个路口和 $56$ 条道路的岛的参考图：  老鼠吱吱很喜欢这座小岛，但是因为某种原因，它的地图被吹走了。但是吱吱想规划它的行程，所以他想知道小岛房子的位置。 幸运的是，它记录了**每一条道路的起点和终点**的观察记录本还在，现在请你推出，共有几种不同的情况使得小岛房子的位置不同。 **注意小岛是环形的，经过旋转完全一样的顺序视为同一种顺序**。

第一行两个整数 $n,m$。 接下来 $n+m-1$ 行，每行两个整数 $u,v$，表示这条道路的起点与终点。如 $u \leq n$，则起点是一所房子，否则是一个路口。对 $v$ 同理。

若干行，第 $i$ 行两个整数 $a_i,b_i$。 假设你的答案由 $k$ 行构成。你的输出表示 答案 $P=a_1^{b_1}a_2^{b_2}\cdots a_k^{b_k}$（也可记作 $\prod_{j=1}^ka_j^{b_j}$）。 你的输出应满足以下要求： - $0\leq k\leq 10^6$ - $1\leq a_i,b_i\leq 10^{18}$ **如果无解，请什么都不要输出**。

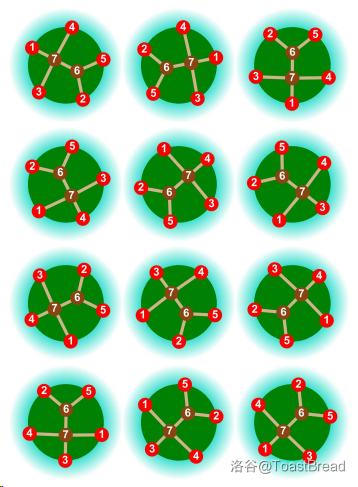
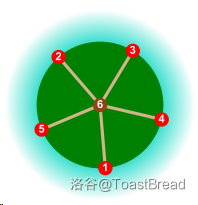
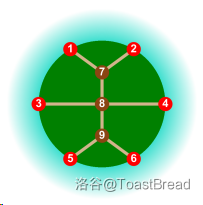
### 【样例 #1 解释】 有 $12$ 种合法的排列，如下图。 使用其他的方式（如 $4^1\times3^1$）也是可以的。 所有排列如下：  ### 【样例 #2 解释】 有 $24$ 种合法的排列，其中一种如下：  算出答案是 $5!=120$ 的很有可能是因为没有考虑旋转后一样的视为同一种方案的问题。 ### 【样例 #3 解释】 有 $24$ 种合法的排列，其中一种如下：  ### 【数据范围】 | $\text{Subtask}$ | 分值 | 特殊性质 | | :----------: | :----------: | :----------: | | $0$ | $0$ | 样例 | | $1$ | $7$ | $n+m\leq 2\times 10^5,m\leq1$ | | $2$ | $20$ | $n+m\leq 2\times 10^5,m\leq10$ | | $3$ | $31$ | $n+m\leq 10^3$ | | $4$ | $42$ | $n+m\leq 2\times 10^5$ | 对于 $100\%$ 的数据： - $2 \leq n,0\leq m$ - $n+m \leq 2\times10^5$