P11355 [eJOI 2023] Teleporters

dXqwq 和 Haitang 在数轴上的两个不同的点 $A,B$，他们想要见面，但是他们只能通过传送器移动。 有 $N$ 个传送器，第 $i$ 个位于坐标轴 $c_i$ 位置，频率为 $f_i$。由于某种原因，只有频率 $\in[L,R]$ 的传送器可以使用。 使用一个传送器会将一个人传送到与其坐标对称的点。形式化地说，一个人传送前后的位置 $x_1,x_2$ 与传送器的位置 $c_i$ 满足 $\frac{x_1+x_2}{2}=c_i$。 dXqwq 和 Haitang 会不断**同时**各自选择一个传送器 $p,q$（不需要相同），进行传送并经历 $|f_p-f_q|$ 的**疲劳值**，直到他们抵达同一位置。整个过程的疲劳值为每次经历的疲劳值的最大值。 给定 $Q$ 次询问，每次给定一组 $[L,R]$，求 dXqwq 和 Haitang 见面的总疲劳值的最小值，或报告他们不可能通过这些传送器见面。

第一行输入两个整数 $N,Q$。 第二行输入 $N$ 个整数 $c_i$。 第三行输入 $N$ 个整数 $f_i$。 接下来 $Q$ 行，每行输入四个整数 $A,B,L,R$，保证 $A\neq B$。

输出一行 $Q$ 个整数，代表每个询问总疲劳值的最小值。特别地，如果不可能见面，输出 ``-1``。

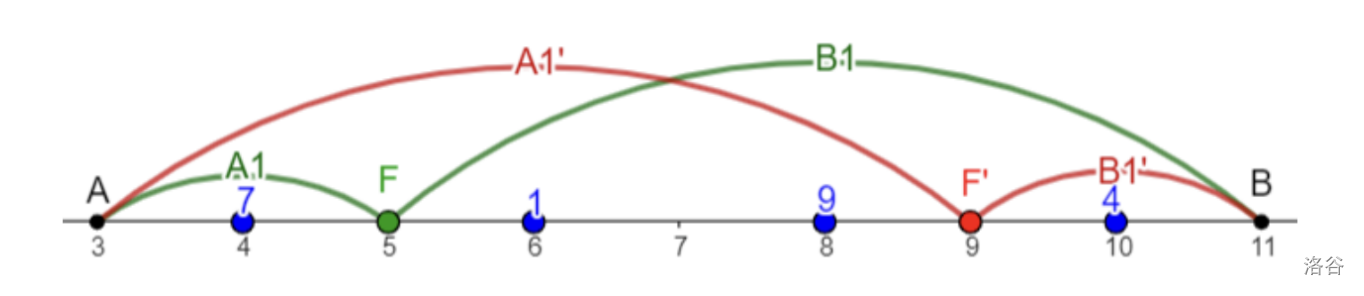
**【样例解释】** 下面为第一组样例的解释。  第一次询问中，如果 dXqwq 选择第二个传送器，Haitang 选择第四个传送器，可以在 $9$ 处见面，疲劳值为 $3$。但如果 dXqwq 选择第一个传送器，Haitang 选择第三个传送器，可以在 $5$ 处见面，疲劳值为 $2$。 第二次询问中，上述的第二种方法由于 $[L,R]$ 的限制不合法。 第三次询问中，只有一个可用的传送器，见面是不可能的。 注意坐标可能是负数。 **【数据范围】** **本题采用捆绑测试。** - Subtask 1（11 pts）：$N,Q\leq 10$，$|c_i|,f_i\leq 50$。 - Subtask 2（10 pts）：$N\leq 100$，$L=1$，$R=10^9$，$|c_i|,f_i\leq 100$。 - Subtask 3（5 pts）：$N=2$，$L=1$，$R=10^9$。 - Subtask 4（9 pts）：$N\leq 10^3$，$L=1$，$R=10^9$，$f_i=1$。 - Subtask 5（6 pts）：$L=1$，$R=10^9$，$f_i=1$。 - Subtask 6（7 pts）：$N\leq 10^3$，$L=1$，$R=10^9$。 - Subtask 7（17 pts）：$L=1$，$R=10^9$。 - Subtask 8（8 pts）：$L=1$。 - Subtask 9（14 pts）：$N,Q\leq 2\times 10^4$。 - Subtask 10（13 pts）：无特殊限制。 对于 $100\%$ 的数据，保证 $2\leq N\leq 5\times 10^4$，$1\leq Q\leq 5\times 10^4$，$1\leq f_i\leq 10^9$，$-10^9\leq c_i,A,B\leq 10^9$，$1\leq L\leq R\leq 10^9$。