P11363 [NOIP2024] Tree Traversal

Xiao Q, a beginner in algorithmic competitions, is learning about tree traversal in graph theory. A tree with $n$ nodes and $n - 1$ edges initially has all nodes unmarked. Its traversal process is as follows: 1. Select a node $s$ as the starting node for traversal and mark it. 2. Suppose the currently visited node is $u$. Find any adjacent node $v$ to $u$ that is unmarked, set $v$ as the new current node, mark it, and repeat Step 2. 3. If in Step 2, all adjacent nodes of $u$ are already marked: if $u = s$, the traversal ends; otherwise, set $u$ to the previous node before traversing $u$ and repeat Step 2. For example, in the following tree, a possible traversal process is: - Select node $1$ as the starting node and mark it. - Node $2$ is adjacent to $1$ and unmarked. Set $2$ as the current node and mark it. - Node $3$ is adjacent to $2$ and unmarked. Set $3$ as the current node and mark it. - All adjacent nodes of $3$ are marked. Return to the previous node $2$. - Node $4$ is adjacent to $2$ and unmarked. Set $4$ as the current node and mark it. - All adjacent nodes of $4$ are marked. Return to the previous node $2$. - All adjacent nodes of $2$ are marked. Return to the previous node $1$. - All adjacent nodes of $1$ are marked, and since $1$ is the starting node, the traversal ends.  $$\text{Pic1: The tree in sample 1}$$ As a creative student, Xiao Q is not satisfied with node-based traversal and begins researching edge-based traversal. Two edges are defined as **adjacent** if they share a common node. Initially, all edges are unmarked. The edge-based traversal process is: 1. Select an edge $b$ as the starting edge for traversal and mark it. 2. Suppose the currently visited edge is $e$. Find any adjacent edge $f$ to $e$ that is unmarked, set $f$ as the new current edge, mark it, and repeat Step 2. 3. If in Step 2, all adjacent edges of $e$ are marked: if $e = b$, the traversal ends; otherwise, set $e$ to the previous edge before traversing $e$ and repeat Step 2. For example, in the above tree, a possible traversal process (where $\{u, v\}$ denotes the edge connecting nodes $u$ and $v$) is: - Select $\{1, 2\}$ as the starting edge and mark it. - $\{1, 2\}$ is adjacent to $\{2, 3\}$, which is unmarked. Set $\{2, 3\}$ as the current edge and mark it. - $\{2, 3\}$ is adjacent to $\{2, 4\}$, which is unmarked. Set $\{2, 4\}$ as the current edge and mark it. - All adjacent edges of $\{2, 4\}$ are marked. Return to the previous edge $\{2, 3\}$. - All adjacent edges of $\{2, 3\}$ are marked. Return to the previous edge $\{1, 2\}$. - All adjacent edges of $\{1, 2\}$ are marked, and since $\{1, 2\}$ is the starting edge, the traversal ends. Xiao Q discovers that if each edge is treated as a new node, and a new edge is created between every pair of edges $e$ and $f$ where $f$ is chosen in Step 2, this generates a new tree with $n-1$ new nodes and $n-2$ new edges. 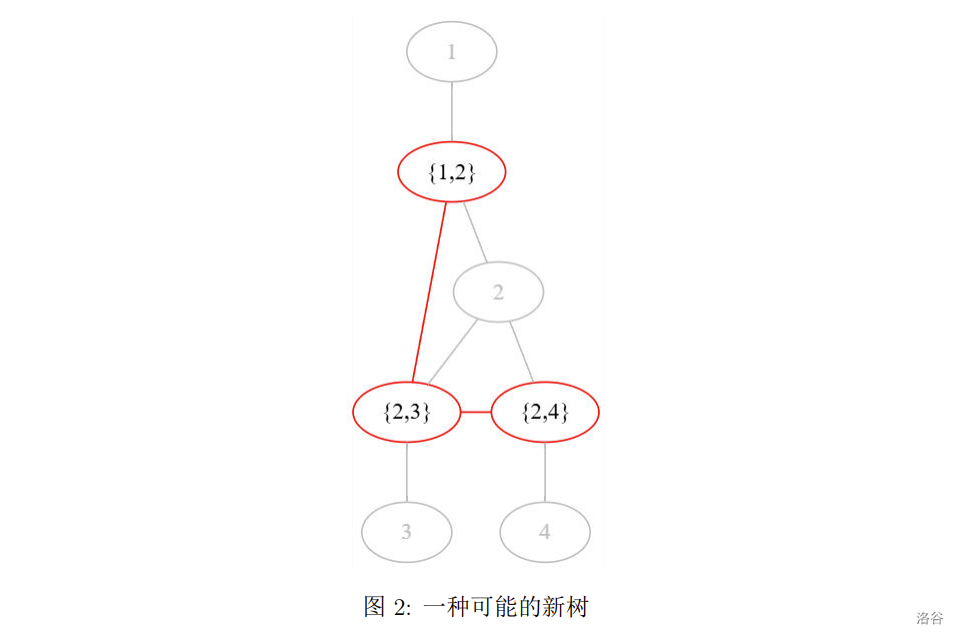For example, the traversal above produces the following new tree (red nodes and edges):  $$\text{Pic2: A possible new tree}$$ Now, Xiao Q has selected $k$ **key edges** among the $n-1$ edges. He wants to know how many distinct new trees can be generated by starting the traversal from any key edge. Two trees are considered different if there exists at least one pair of new nodes connected by an edge in one tree but not in the other. **Since the result may be large, output the answer modulo $10^9+7$.**

**The problem contains multiple test cases.** The first line of input contains two integers $c$ and $T$, representing the test case ID and the number of test cases. In sample inputs, $c$ indicates that the sample shares the same data range as test case $c$. This is followed by $T$ test cases, each formatted as: - The first line contains two integers $n$ and $k$, representing the number of nodes in the tree and the number of key edges selected. - The next $n - 1$ lines each contain two integers $u_i$ and $v_i$, representing the nodes connected by the $i$-th edge in the tree. - The next line contains $k$ integers $e_1, e_2, \dots, e_k$, representing the indices of the key edges. All key edge indices are distinct.

For each test case, output one line containing the result modulo $10^9 + 7$.

### Explanation **【Sample 1 Explanation】** Two possible new trees: 1. New edges between $\{1, 2\}$ and $\{2, 3\}$, and between $\{2, 3\}$ and $\{2, 4\}$. 2. New edges between $\{1, 2\}$ and $\{2, 4\}$, and between $\{2, 4\}$ and $\{2, 3\}$. **【Sample 2 Explanation】** Three possible new trees: 1. New edges between $\{1, 2\}$ and $\{1, 3\}$, $\{1, 2\}$ and $\{2, 4\}$, $\{2, 4\}$ and $\{2, 5\}$ (starting from $\{1, 2\}$). 2. New edges between $\{1, 2\}$ and $\{1, 3\}$, $\{1, 2\}$ and $\{2, 5\}$, $\{2, 5\}$ and $\{2, 4\}$ (starting from $\{1, 2\}$ or $\{2, 4\}$). 3. New edges between $\{1, 2\}$ and $\{1, 3\}$, $\{1, 2\}$ and $\{2, 4\}$, $\{1, 2\}$ and $\{2, 5\}$ (starting from $\{2, 4\}$). **【Additional Samples】** Samples 3 to 12 are provided in attachments (traverse3.in to traverse12.ans), corresponding to test cases 4, 7, 11, 13, 15, 16, 18, 19, 22, and 24. **【Data Range】** For all test data: - $1 \leq T \leq 10$; - $2 \leq n \leq 10^5$; - $1 \leq k < n$; - For every $i$ ($1 \leq i \leq n - 1$), $1 \leq u_i, v_i \leq n$, forming a valid tree; - For every $i$ ($1 \leq i \leq k$), $1 \leq e_i < n$, all distinct. | Test Case Range | $n$ | $k$ | Special Properties | | :--------------: | :--------------: | :--------------: | :--------------: | | $1\sim 3$ | $\leq 5$ | $\leq 1$ | None | | $4\sim 6$ | $\leq 10^5$ | $\leq 1$ | None | | $7\sim 10$ | $\leq 10^5$ | $\leq 2$ | None | | $11,12$ | $\leq 500$ | $\leq 8$ | None | | $13,14$ | $\leq 10^2$ | $