P11364 [NOIP2024] Tree Query

One day, Xiao S and her friend Xiao N studied a tree with $n$ nodes. This is a rooted tree with root node numbered $1$. The depth $\text{dep}_u$ of a node $u$ is defined as the **number of nodes** on the simple path from $u$ to $1$. Additionally, $\text{LCA*}(l, r)$ is defined as the lowest common ancestor (LCA) of all nodes with numbers in $[l, r]$, i.e., the deepest node that is an ancestor of all nodes $l, l + 1, \dots, r$. Xiao N posed $q$ queries about this tree. For each query, he provides three parameters $l, r, k$, asking for the maximum depth among the LCAs of all continuous subintervals of $[l, r]$ with length at least $k$. Formally, compute: $$ \max_{l\le l'\le r'\le r \land r'-l'+1\ge k}\text{dep}_{\text{LCA*}(l', r')} $$ Your task is to help Xiao S answer these queries.

The first line contains a positive integer $n$, the number of nodes in the tree. The next $n - 1$ lines each contain two positive integers $u$ and $v$, representing an edge between nodes $u$ and $v$. The $(n + 1)$-th line contains a positive integer $q$, the number of queries. The next $q$ lines each contain three positive integers $l, r, k$, describing a query.

For each query, output one line containing the answer.

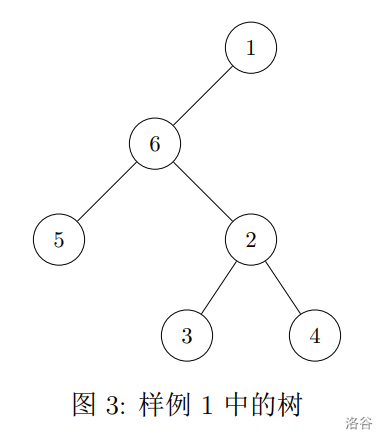
## Explanation **【Sample 1 Explanation】**  $\text{Pic 3: The tree in sample 1}$ + For the first query: - $\text{LCA*}(2, 3) = 2$, $\text{LCA*}(3, 4) = 2$, $\text{LCA*}(4, 5) = 6$. - The depth of node $2$ is $3$, and the depth of node $6$ is $2$. - Thus, the answer is $\max\{3, 3, 2\} = 3$. + For the second query: - The answer is the maximum depth among nodes $1, 2, 3, 4$, which is $4$. + For the third query: - $\text{LCA*}(1, 3) = 1$, $\text{LCA*}(2, 4) = 2$, $\text{LCA*}(3, 5) = 6$, $\text{LCA*}(4, 6) = 6$. - The depth of node $2$ is $3$, which remains the maximum, so the answer is $3$. **【Sample 2】** See the attached files `query/query2.in` and `query/query2.ans`. This sample satisfies $n, q \leq 500$. **【Sample 3】** See the attached files `query/query3.in` and `query/query3.ans`. This sample satisfies $n, q \leq 10^5$ and the tree forms a chain. **【Sample 4】** See the attached files `query/query4.in` and `query/query4.ans`. This sample satisfies $n, q \leq 5 \times 10^5$. **【Data Range】** For all test data: - $1 \leq n, q \leq 5 \times 10^5$ - $1 \leq l \leq r \leq n$ - $1 \leq k \leq r - l + 1$ | Test Case Range | $n, q \leq$ | Special Constraints | | :-------------: | :-------------: | :-------------: | | $1\sim2$ | $500$ | None | | $3\sim5$ | $5000$ | None | | $6\sim9$ | $10^5$ | Property A | | $10\sim13$ | $5 \times 10^5$ | Property A | | $14\sim16$ | $5 \times 10^5$ | Property B | | $17\sim20$ | $10^5$ | None | | $21\sim25$ | $5 \times 10^5$ | None | - **Property A**: The tree is a chain (root has degree $1$). - **Property B**: For every query, $k = r - l + 1$. --- Translated by DeepSeek R1