P11442 [Code+#6] 坐标转换
题目背景
搬运自 [Code+ 第 6 次网络赛](https://gitlink.org.cn/thusaa/codeplus6/)。
题目描述
在视频编码中,往往需要将一帧画面分块。
为了简化问题,我们考虑将一幅图片看作 $2^n\times 2^n$ 的网格。为了对图片进行处理,编码器往往会遍历每个格子,但遍历格子的方式在不同的应用中是不同的。
其中一种方式叫做光栅遍历,就是按照从左到右,从上到下的顺序依次进行标号。下图是一个 $8\times 8$ 的例子:
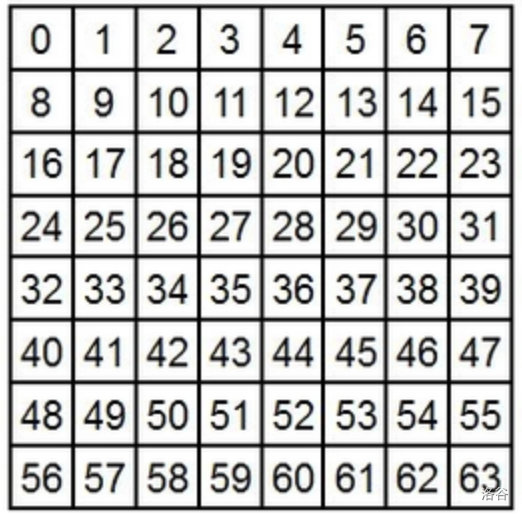
另一种方式叫做 Z 字型遍历。先看一个 $8\times 8$ 的例子:

可以构造性的给出描述:
1.对于 $2^0\times2^0$ 的网格,直接遍历;
2.对于 $2^k\times2^k(k>0)$ 的网格,将其横着从中间、竖着从中间各分成两半,形成 $4$ 个 $2^{k-1}\times2^{k-1}$ 的方格,这四个方格按照左上、右上、左下、右下的顺序依次遍历。
输入格式
输入的第一行为两个整数 $n,m$,其中 $2^n$ 为矩形的边长,$m$ 为询问次数。
接下来 $m$ 行,每行是一个询问,每个询问给出一个方格,方式有两种,如下:
- `Z x`:给出 Z 字形遍历中标号是 $x$ 的方格。
- `R x`:给出光栅遍历中标号是 $x$ 的方格。
保证存在标号为 $x$ 的方格。
输出格式
对于每种询问,请输出一行一个正整数,表示在另一种遍历方式中,给出格子的标号。
说明/提示
### 样例解释
如上图所示。
### 数据范围
对于所有数据,保证 $1\le n\le 30$,$1\le m\le 5\times10^5$。