P11473 名字取好了吗

众所周知，一次签到很可能伴随着一次签退，只有同时签到和签退才算出勤。 这是一道签退题，请通过这道题以证明你打了这次比赛。

在二维平面上有 $n$ 个点，第 $i$ 个点的坐标为 $(x_i,y_i)$。若对于所有 $1\le i\le n$，连接 $i$ 号点和 $(i\ \text{mod}\ n)+1$ 号点，将构成一个凸包。 平面中有 $2n-3$ 条线段，第 $i$ 条线段连接着 $u_i$ 号点和 $v_i$ 号点，其权值为 $w_i$。除了端点外，**所有线段互不相交**。 当你从一个点经过若干条线段到达另一个点时（**你不能经过一个点多次**），你经过的路径上两条相邻的线段共包含三个点，这三个点构成一个三角形（可能退化为线段），在构成的若干三角形中，若某个三角形内部没有任何其他线段，则称其为**纯净三角形**。你可以在【说明/提示】部分的【题意图解】看到更详细的附带图片的解释。 你从一个点经过若干条线段到达另一个点花费的代价为经过的所有线段的权值和与该路径构成的所有纯净三角形面积和的 $2k$ 倍的和，记从 $i$ 号点到 $j$ 号点所需花费的最小代价为 $f(i,j)$。 形式化的，从 $i$ 号点到 $j$ 号点的过程中，设你经过的点的编号集合为 $V$，你经过的线段的编号集合为 $E$，$H(V,E)$ 表示 $V$ 与 $E$ 构成的所有纯净三角形的面积和，则 $f(i,j)$ 为 $\sum\limits_{x\in E}w_x+2k\times H(V,E)$ 的最小值。 你需要求出 $\operatorname*{xor}\limits_{i=1}^{n}\operatorname*{xor}\limits_{j=i+1}^{n}f(i,j)$，即所有 $f(i,j)$ 的异或和。

第一行两个整数 $n,k$。 接下来 $n$ 行，每行两个整数，第 $i$ 行表示 $x_i,y_i$。 接下来 $2n-3$ 行，每行三个整数，第 $i$ 行表示 $u_i,v_i,w_i$。

输出一行一个整数，表示答案。

对于 $100\%$ 的数据，$3\le n\le2500$，$1\le u_i,v_i\le n$，$u_i\not=v_i$，$0\le x_i,y_i,k\le10^6$，$0\le w_i\le10^9$。 容易证明在题目限制下，$f(i,j)$ 总是整数。 注意凸包上可能存在三点共线。 **【样例 1 解释】** $f(1,2)=1$，$f(1,3)=4$，$f(1,4)=6$，$f(2,3)=2$，$f(2,4)=6$，$f(3,4)=4$，$1\operatorname{xor}4\operatorname{xor}6\operatorname{xor}2\operatorname{xor}6\operatorname{xor}4=3$。 **【样例 2 解释】** $f(1,2)=1$，$f(1,3)=4$，$f(1,4)=8$，$f(2,3)=2$，$f(2,4)=6$，$f(3,4)=4$，$1\operatorname{xor}4\operatorname{xor}8\operatorname{xor}2\operatorname{xor}6\operatorname{xor}4=13$。 **【样例 3 解释】** $f(1,2)=1000002$，$f(1,3)=1$，$f(1,4)=10002$，$f(2,3)=1$，$f(2,4)=2$，$f(3,4)=1$，$1000002\operatorname{xor}1\operatorname{xor}10002\operatorname{xor}1\operatorname{xor}2\operatorname{xor}1=1008979$。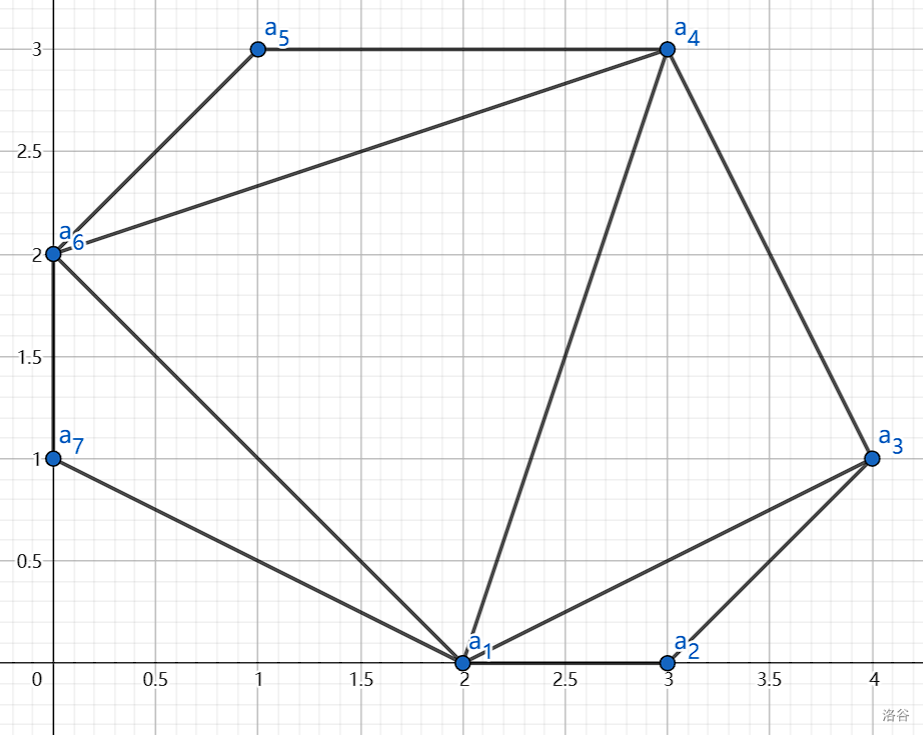 **【题意图解】**  这是一个满足题目限制的凸包。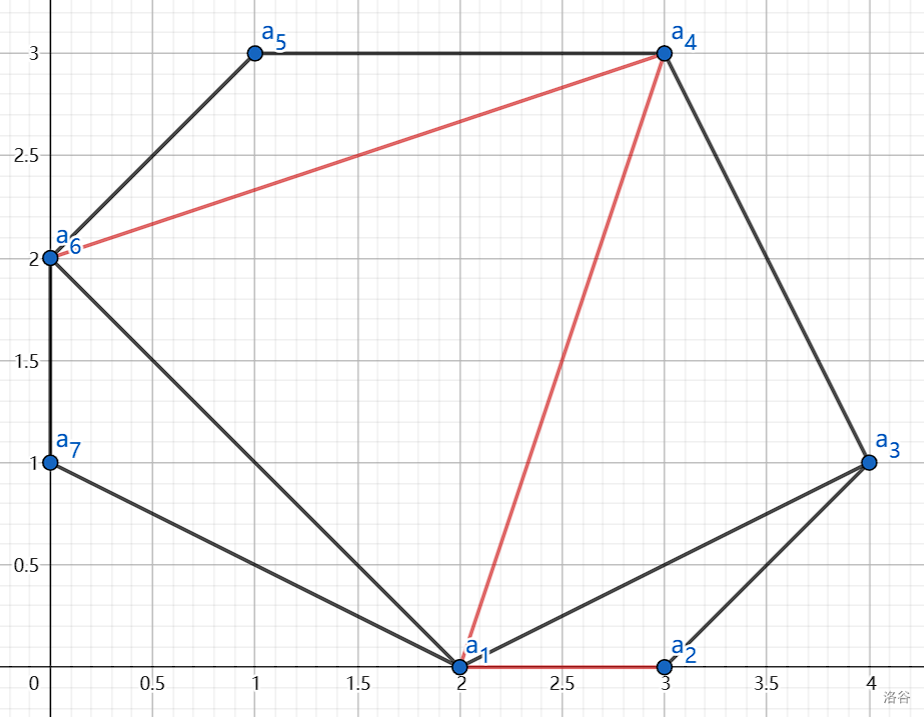  上图红色部分是一条从 $a_2$ 到 $a_6$ 的路径。  上图红色部分是路径中前两条线段包含的三个点构成的三角形。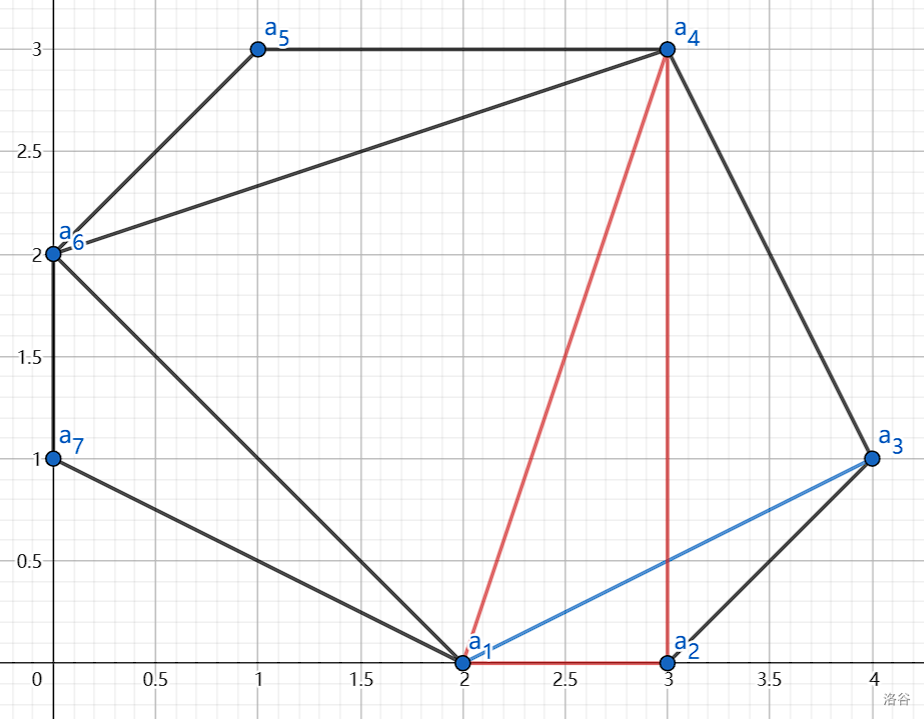  如上图所示，红色三角形内部有蓝色线段的一部分，故该三角形不是纯净三角形。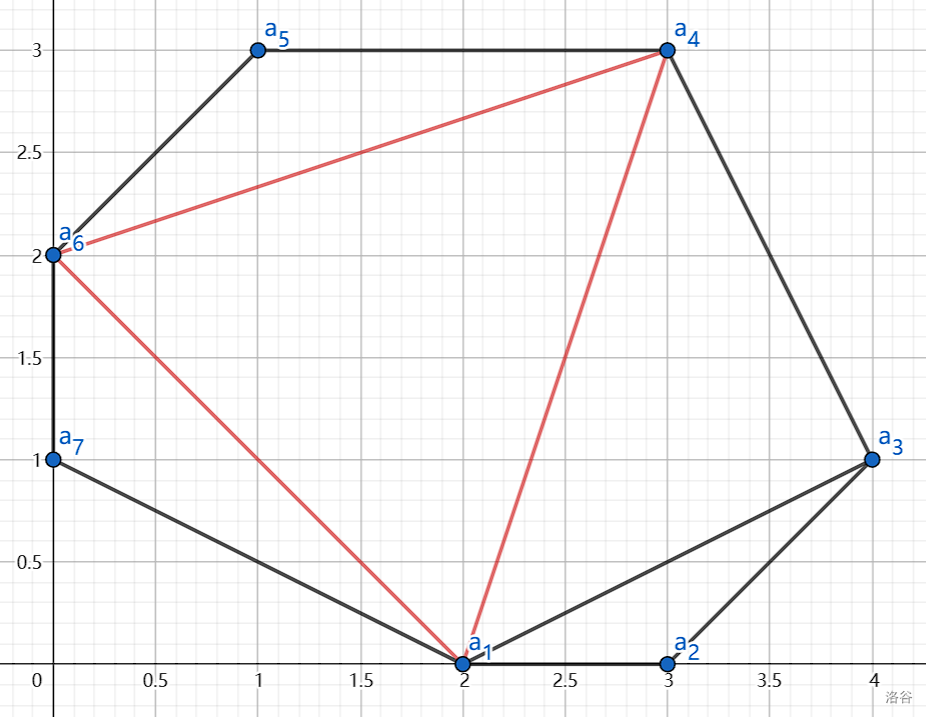  上图红色部分是路径中后两条线段包含的三个点构成的三角形。可以看到红色三角形内部没有任何其他线段，故该三角形是纯净三角形。 对于这条路径，花费的代价为路径上三条线段的权值和加上后一个三角形的面积的 $2k$ 倍。