P11489 [BalticOI 2023] Astronomer

给定平面上 $n$ 个整点，一个正整数 $k$ 和非负整数 $s,t$，在所有至少覆盖了 $k$ 个点的圆中，设其半径为 $r$，圆心离原点（即 $(0,0)$）距离为 $d$，试求出 $tr+sd$ 的最小值。 本题中的距离为欧几里得距离。

第一行四个非负整数 $k,n,s,t$。 接下来 $n$ 行，第 $i$ 行两个整数 $x_i,y_i$ 表示第 $i$ 个点的坐标。

一行一个实数表示答案。若你的输出和标准答案的相对误差或绝对误差不超过 $\varepsilon=10^{-6}$（在部分子任务中，$\varepsilon$ 的值有变化），你的输出将被判定为正确。

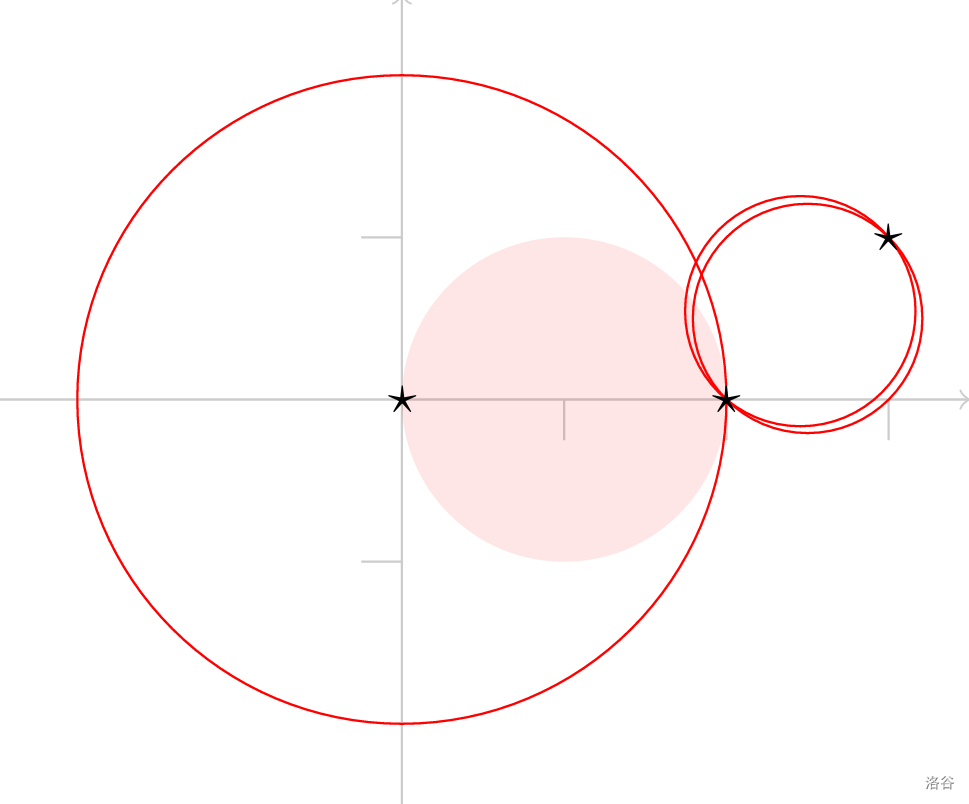
**【样例解释】**  如图，样例 #3 中，最优方案是选择以 $(1,0)$ 为圆心而半径为 $r=1$ 的圆（图中粉色实心圆），代价为 $t\cdot 1+s\cdot 1=1\,000$。 图中的其它三个圆展示了样例 #1、样例 #2，样例 #4 的最优方案。 **【数据范围】** 对于 $100\%$ 的数据，$1\le k\le n\le 700$，$-10^9\le x_i,y_i\le 10^9$，$0\le s,t\le 10^9$。 | 子任务编号 | 分值 | 特殊限制 | | :----------: | :----------: | :----------: | | $1$ | $8$ | $t\le s$ | | $2$ | $9$ | $n\le 50$ 且 $s=0$ | | $3$ | $18$ | $s=0$ | | $4$ | $13$ | $n\le 50$ | | $5$ | $14$ | $n\le 350$ | | $6$ | $15$ | $\varepsilon=0.1$ | | $7$ | $23$ | 无特殊限制 |