P11514 [CCO 2024] Treasure Hunt

翻译自 [CCO](https://cemc.uwaterloo.ca/resources/past-contests?contest_category=80) 的 [2024 P1](https://dmoj.ca/problem/cco24p1)。

佩里海盗正在航行七大洋！他有一张由 $N$ 个岛屿和 $M$ 条海路组成的地图。第 $i$ 条海路连接岛屿 $a_i$ 和 $b_i$，双向通行的费用为 $c_i$ 金币。与海怪交战代价不菲。为了寻找下一个大笔战利品，佩里已经侦查过每个岛屿，确定第 $i$ 个岛上有一个装有 $v_i$ 金币的宝箱。 他打算航行一段（可能为空）的海路，从岛屿 $x$ 出发到岛屿 $y$ 结束。旅程结束时，他会打开岛屿 $y$ 的宝箱并获得战利品。这里的问题是：佩里并不知道自己当前在哪个岛上！因此，对于每个可能的起始岛 $x$，他想知道从该岛出发所有可能旅程中能够获得的最大净收益（假设他有足够的金币支付沿途的通行费用；他只关心下一次旅程的净利润）。

第一行两个整数 $n, m$。 第二行 $n$ 个整数 $v_i$。 往后 $m$ 行每行三个整数 $a_i, b_i, c_i$，其描述了一条海路 $i$。 保证无重边无自环。

$n$ 行，每行一个整数，第 $i$ 行的整数代表以点 $i$ 为起点岛屿所获得的最大可能的硬币数。

### 数据范围 | Subtask | 分数 | 约束 | | :----------: | :----------: | :----------: | | Subtask $0$ | $0$ | 样例 | | Subtask $1$ | $20$ | $1 \le n \le 3000$，$0 \le m \le 3000$ | | Subtask $2$ | $20$ | $1 \le n \le 10^6$，$0 \le m \le 10^6$，对于每个岛屿 $i$，$c_i=0$ 或 $c_i=10^9$ | | Subtask $3$ | $28$ | $1 \le n \le 10^6$，$0 \le m \le 10^6$，任意一对岛屿之间恰好有一条路径 | | Subtask $4$ | $32$ | 无特殊限制 | 对于 $100\%$ 的数据，$1 \le n \le 10^6$，$0 \le m \le 10^6$，$0 \le v_i,c_i \le 10^9$，$1 \le a_i,b_i \le n$。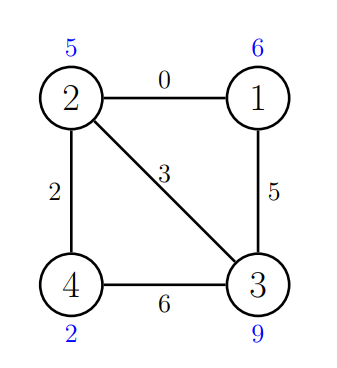 ### 样例解释 #1  对于第一个和第三个岛屿，最好待在岛上并打开岛上的箱子。 对于第二个岛屿，佩里可以前往第一个岛屿并打开那里的箱子。这将带来 $6 - 0 = 6$ 枚硬币的净收益，是最佳的净收益。 对于第四个岛屿，佩里可以前往第二个和第三个岛屿并打开那里的箱子。这将带来 $9 - 2 - 3 = 4$ 枚硬币的净收益，是最佳的净收益。