P1155 [NOIP 2008 Senior] Two-Stack Sorting

Tom has been studying an interesting sorting problem. As shown in the figure, by using 2 stacks $S_1$ and $S_2$, Tom hopes to sort the input sequence in ascending order using the following 4 operations.  - Operation $\verb!a!$: Push the first element of the input sequence onto stack $S_1$. - Operation $\verb!b!$: Pop the top element of $S_1$ to the output sequence. - Operation $\verb!c!$: Push the first element of the input sequence onto stack $S_2$. - Operation $\verb!d!$: Pop the top element of $S_2$ to the output sequence. If a permutation $P$ of $1\sim n$ can, via a series of valid operations, produce the output sequence $(1,2,\cdots,n-1,n)$, then Tom calls $P$ a "two-stack sortable permutation." For example, $(1,3,2,4)$ is a "two-stack sortable permutation," while $(2,3,4,1)$ is not. The following figure shows an operation sequence that sorts $(1,3,2,4)$: $\texttt {a,c,c,b,a,d,d,b}$.  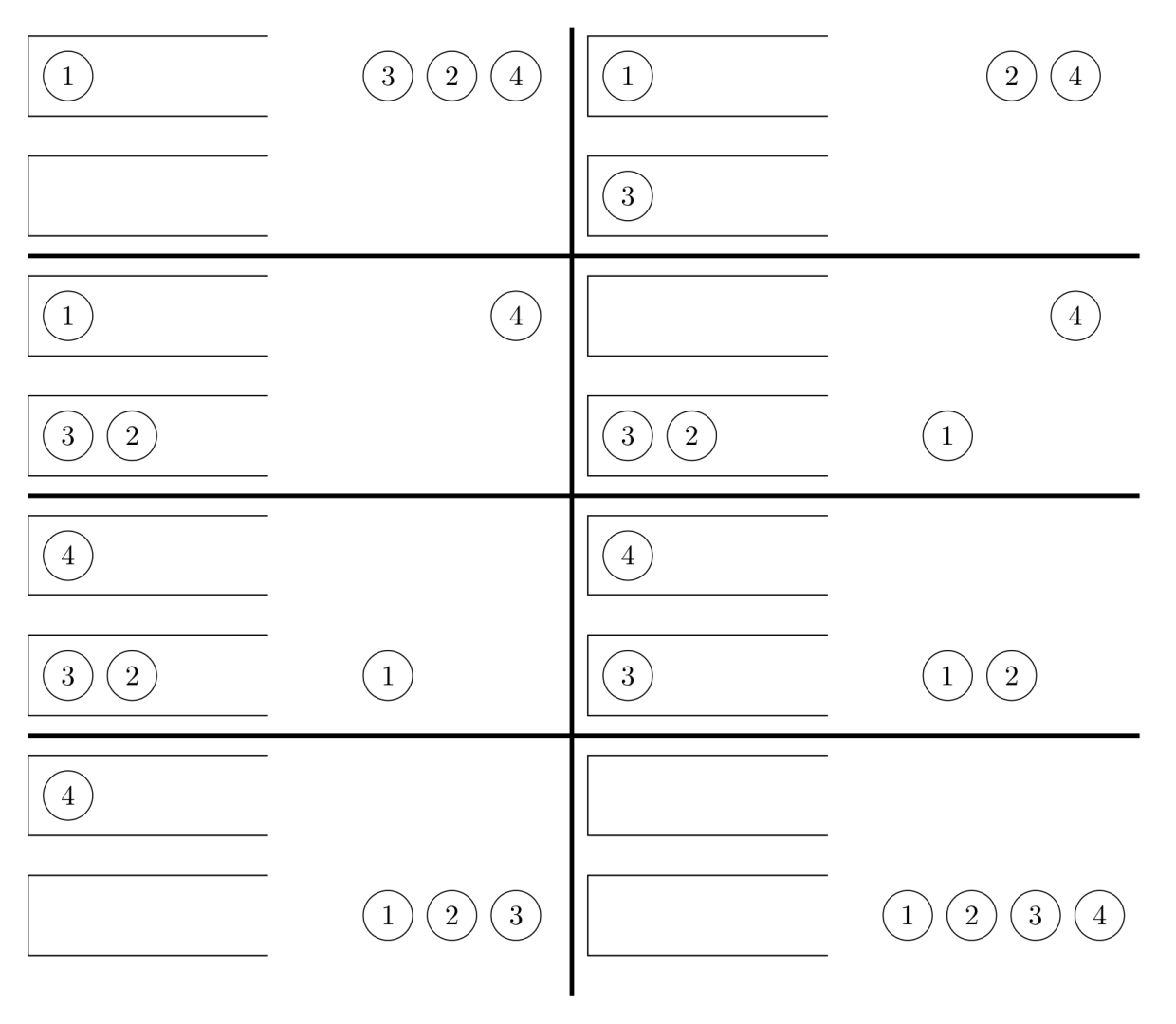Of course, there may be multiple such operation sequences. For the above example $(1,3,2,4)$, $\texttt{a,b,a,a,b,b,a,b}$ is another valid operation sequence. Tom wants to know the lexicographically smallest operation sequence among them.

The first line contains an integer $n$. The second line contains $n$ positive integers separated by spaces, forming a permutation of $1\sim n$.

Output a single line. If the input permutation is not a "two-stack sortable permutation," output `0`. Otherwise, output the lexicographically smallest operation sequence, with a space between every two operations and no trailing space at the end.

$30\%$ of the testdata satisfy: $n\le10$. $50\%$ of the testdata satisfy: $n\le50$. $100\%$ of the testdata satisfy: $n\le1000$. 2021.06.17 strengthened by [SSerxhs](https://www.luogu.com.cn/user/29826). Hack testdata are separated into a single subtask to avoid confusion. NOIP 2008 Senior Problem 4. Translated by ChatGPT 5