P1158 [NOIP 2010 Junior] Missile Interception

After $11$ years of preparation, a certain country has developed a new missile interception system. Any missile whose distance to the system does not exceed its working radius can be successfully intercepted. When the working radius is $0$, it can intercept missiles that are exactly at the same position as the system. However, the system has a limitation: each set of the system can have its working radius set only once per day. The usage cost for that day is the sum of the squares of the working radii of all systems. One day, radar detected incoming enemy missiles. Since the system is still in the trial phase, only two systems are deployed. If the requirement is to intercept all missiles, compute the minimum usage cost for that day.

The first line contains $4$ integers $x_1, y_1, x_2, y_2$, separated by a single space, indicating that the coordinates of the two missile interception systems are $(x_1, y_1)$ and $(x_2, y_2)$. The second line contains $1$ integer $N$, the number of missiles. The next $N$ lines each contain two integers $x, y$, separated by a single space, indicating the coordinates $(x, y)$ of a missile. Different missiles may share the same coordinates.

A single integer, the minimum usage cost for that day.

- The square of the distance between two points $(x_1, y_1)$ and $(x_2, y_2)$ is $(x_1-x_2)^2+(y_1-y_2)^2$. - The sum of the squares of the two working radii $r_1, r_2$ means squaring them separately and then summing, i.e., $r_1^2+r_2^2$. Explanation for Sample $1$: To intercept all missiles with minimum usage cost, the squares of the two systems’ working radii are $18$ and $0$. 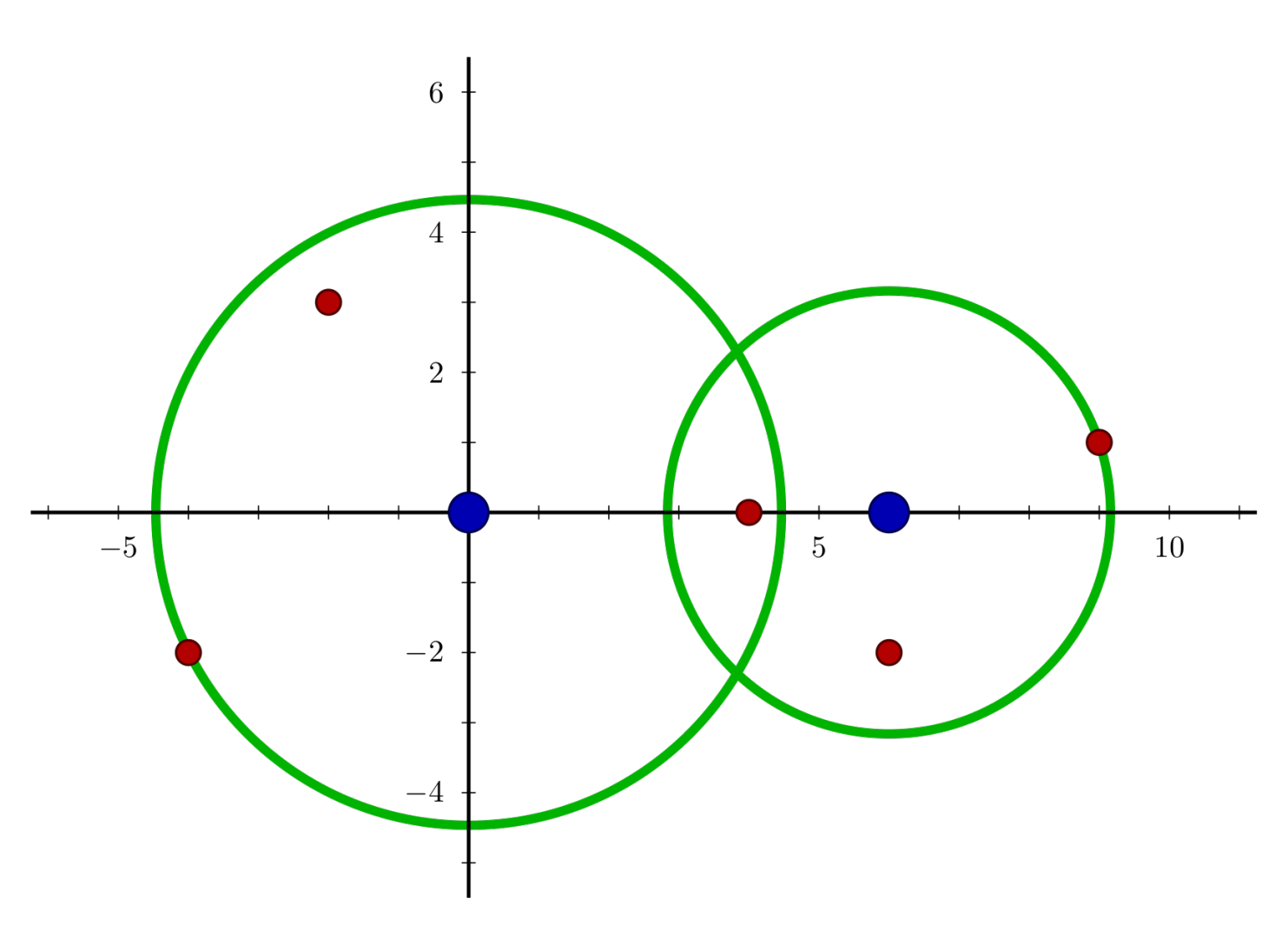Explanation for Sample $2$: The positions of the interception systems and the missiles are shown below. To intercept all missiles with minimum usage cost, the squares of the two systems’ working radii are $20$ and $10$.  Constraints: - For $10\%$ of the testdata, $N=1$. - For $20\%$ of the testdata, $1\le N\le 2$. - For $40\%$ of the testdata, $1\le N\le 100$. - For $70\%$ of the testdata, $1\le N\le 1000$. - For $100\%$ of the testdata, $1\le N\le 10^5$, and the absolute values of all coordinate components do not exceed $1000$. NOIP 2010 Junior, Problem 3. Translated by ChatGPT 5