P11594 [NOISG 2018 Finals] Collecting Mushrooms

译自 [NOISG 2018 Finals A. Collecting Mushrooms](https://github.com/noisg/sg_noi_archive/tree/master/2018/tasks/collectmushrooms)。

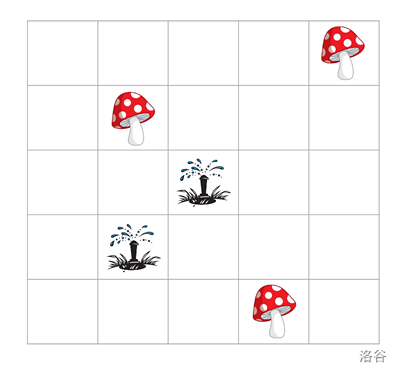
螃蟹 Lim Li 在她的花园里打造了一个蘑菇种植园。这个蘑菇种植园可以看成一个 $R$ 行 $C$ 列的网格，其中每一格要么是空的，要么有一朵蘑菇，要么有一个洒水器。 举个例子，一个 $R=5,C=5$ 的蘑菇种植园可能是长这样子的：  一朵蘑菇和一个洒水器之间的距离被定义为它们的横坐标差的绝对值与纵坐标差的绝对值的较大值。换句话说，假设一朵蘑菇位于 $X_m$ 行 $Y_m$ 列，一个洒水器位于 $X_s$ 行 $Y_s$ 列，那么它们之间的距离为 $\max(|X_m-X_s|,|Y_m-Y_s|)$。 一个洒水器只能浇到距离自己不超过 $D$ 的蘑菇。下图展示了 $D=1$ 时洒水器可以浇到的区域：  一朵蘑菇如果可以被至少 $K$ 个洒水器浇到，则我们称它是**好蘑菇**。你需要帮 Lim Li 计数在她的蘑菇种植园里有多少朵**好蘑菇**。

第一行包含四个整数 $R,C,D,K$，含义如题意所述。 接下来 $R$ 行，每行 $C$ 个字符，描述一个蘑菇种植园。每个字符表示一个格子： - `.` 表示一个空格子。 - `M` 表示一个有一朵蘑菇的格子。 - `S` 表示一个有一个洒水器的格子。

一行一个整数，表示**好蘑菇**的数量。

### 样例 #1 解释 所有洒水器可以浇到的距离范围都是 $1$，也就是每个洒水器都能且仅能洒到与自己八连通的格子。只有位于 $(2,2)$ 的蘑菇可以被浇到水。 这组样例满足子任务 $3,4,6$。 ### 样例 #2 解释 唯一的洒水器可以浇到的距离范围是 $4$，所以可以浇到所有蘑菇。 这组样例满足子任务 $1,2,4,6$。 ### 样例 #3 解释 所有蘑菇都需要被两头的洒水器浇到才能成为**好蘑菇**。因为洒水器可以浇到的距离范围都是 $5$，所以只有从左往右第二朵和第三朵蘑菇满足**好蘑菇**的要求。 这组样例满足子任务 $4,5,6$。 ### 样例 #4 解释 因为洒水器可以浇到的距离范围都是 $2$，所以只有位于 $(2,2)$ 和 $(5,4)$ 的蘑菇可以同时被两个洒水器浇到。 这组样例满足子任务 $4,6$。 ### 子任务 对于 $100\%$ 的数据，$2\le RC\le 5\times 10^5$，$1\le D\le \max(R,C)$，$1\le K\le RC$。保证种植园中至少有一朵蘑菇和一个洒水器。 | 子任务 | 得分 | 数据范围及特殊性质 | | :----------: | :----------: | :----------: | | $1$ | $9$ | $1\le R,C\le 100$，$D=\max(R,C)$，$K=1$ | | $2$ | $10$ | $1\le R,C\le 100$，$D=\max(R,C)$ | | $3$ | $18$ | $1\le R,C\le 100$，$D=1$，$K=1$ | | $4$ | $23$ | $1\le R,C\le 500$，洒水器和蘑菇的数量均少于 $500$ | | $5$ | $19$ | $R=1$ | | $6$ | $21$ | 无特殊限制 |