P11596 [NOISG 2018 Finals] Lightning Rod
题目背景
译自 [NOISG 2018 Finals C. Lightning Rod](https://github.com/noisg/sg_noi_archive/tree/master/2018/tasks/lightningrod)。
题目描述
新加坡的城市天际线可以看成一个平面直角坐标系,第 $i$ 栋大楼的顶端是点 $(X_i,Y_i)$。
一根避雷针可以安装在大楼的顶端上。它的保护区域为从该大楼顶端向左下方和右下方作两条与坐标轴呈 $45^\circ$ 的射线所产生的 $\frac{1}{4}$ 平面。所有顶端在该保护区域内或落在保护区域边缘上的大楼都可以被保护到。
换句话说,若避雷针安装在大楼 $i$ 上,则所有且仅所有满足 $|X_i-X_j|\le Y_i-Y_j$ 的大楼 $j$ 可以被该避雷针保护到。
你的任务是找出最少的安装避雷针数量,使得所有大楼都可以被至少一根避雷针保护到。
输入格式
第一行一个正整数 $N$,表示大楼的总数。
接下来 $N$ 行每行两个正整数 $X_i,Y_i$,表示第 $i$ 栋大楼的顶端是 $(X_i,Y_i)$。**保证 $X_i$ 按照输入顺序单调不递减**。
注意:本题输入量较大,请使用较快的输入方式。我们在下发文件中下发了三种语言实现的快速读入模板。
输出格式
一行一个整数,表示最少的安装避雷针数量。
说明/提示
### 样例 #1 解释
所有大楼都需要安装避雷针。
这组样例满足所有子任务。
### 样例 #2 解释
在大楼 $2$ 的顶端安装避雷针。
这组样例满足子任务 $2$ 至 $7$。
### 样例 #3 解释
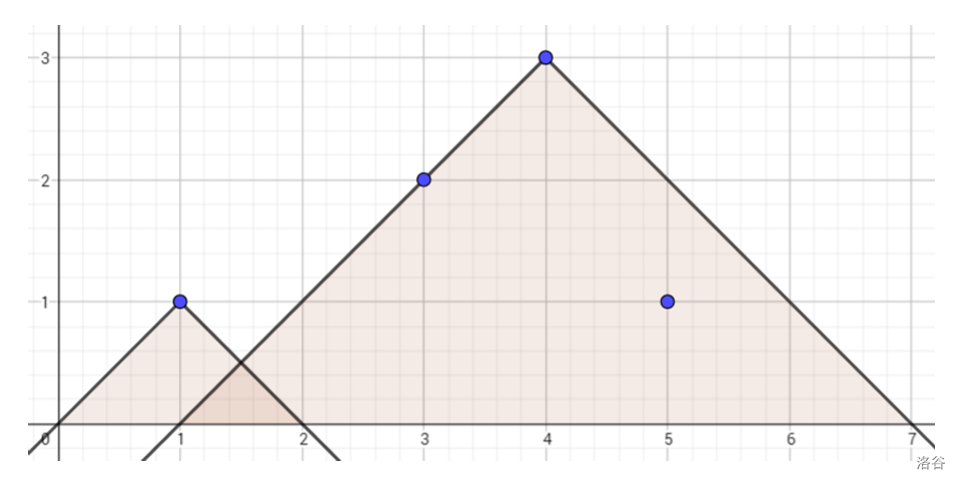
如图所示,在大楼 $1$ 和大楼 $3$ 的顶端安装避雷针。
这组样例满足子任务 $3,4,5,7$。
### 子任务
对于 $100\%$ 的数据,$2\le N\le 10^7$,$0\le X_i,Y_i\le 10^9$。
| 子任务 | 得分 | $N$ | $X_i,Y_i$ |
| :----------: | :----------: | :----------: | :----------: |
| $1$ | $4$ | 无特殊限制 | $Y_i=1$ |
| $2$ | $7$ | $=2$ | 无特殊限制 |
| $3$ | $12$ | $\le20$ | 无特殊限制 |
| $4$ | $21$ | $\le 2\times 10^3$ | 无特殊限制 |
| $5$ | $26$ | $\le 2\times 10^5$ | 无特殊限制 |
| $6$ | $10$ | 无特殊限制 | $X_i=i,Y_i\le 1$ |
| $7$ | $20$ | 无特殊限制 | 无特殊限制 |