P11597 [NOISG 2018 Finals] City Mapping【缺样例】

译自 [NOISG 2018 Finals D. City Mapping](https://github.com/noisg/sg_noi_archive/tree/master/2018/tasks/citymapping)。 ---------------- 当你在洛谷提交本题时，需要注意： - 本题仅支持 C++ 系列语言。 - 你的代码中不应该包含头文件 `citymapping.h`。 - 你的代码中应当有如下两行函数声明： ```cpp long long get_distance(int X, int Y); void find_roads(int N, int Q, int A[], int B[], int W[]); ``` 如遇评测问题，请联系搬题人。

**这是一道交互题。** Silvermill 市是一座有 $N$ 个路口和 $N-1$ 条道路的城市。其中道路的编号为 $0$ 到 $N-2$。 第 $i$ 条道路双向连接了 $(A_i,B_i)$ 两个路口，从任意方向通过这条道路都需要花费 $W_i$ 分钟。保证任意两个路口之间都能通过道路互相到达。 为了避免交通堵塞，Silvermill 市的**每个路口连接的道路不会超过 $3$ 条**。 你的任务是画出 Silvermill 市的地图，也就是找出所有 $N-1$ 条道路的 $(A_i,B_i,W_i)$。 为了达到这个目的，你可以询问市长至多 $Q$ 次从任意一个路口 $X$ 到任意一个路口 $Y$ 最少需要多少分钟。 ### 实现细节 在本题中，**你不需要，也不应该实现主函数**。 你需要实现如下函数： ```cpp void find_roads(int N, int Q, int A[], int B[], int W[]) ``` 该函数包含两个输入参数和三个输出参数，将在评测时被运行恰好一次。输入参数为 $N,Q$，分别表示路口的数量和最大询问次数；输出参数为 $A,B,W$，你需要确定城市中的 $N-1$ 条道路，按题意中的含义以数组 $A,B,W$ 的形式返回。返回道路的顺序可以是任意的，同一道路端点的顺序也可以是任意的。 注意数组的下标是从 $0$ 开始的。 你可以调用下面的函数来完成任务： ```cpp long long get_distance(int X, int Y) ``` 该函数将返回一个整数，表示从路口 $X$ 到路口 $Y$ 最少需要多少分钟。如果你调用此函数超过 $Q$ 次，或提供无效的路口编号作为参数，程序将立刻终止，你将得到 Wrong Answer 的评测状态。

示例测试程序如下方式读入数据： 第一行三个整数 $N,Q,S$，分别表示路口的数量、最大询问次数和子任务编号。 之后是 $N-1$ 行，每行三个整数 $(A_i,B_i,W_i)$，描述一条道路。

示例测试程序可能会产生的输出如下： - `Wrong Input Format`，意味着对示例测试程序的输入格式有误。 - `Wrong Answer: Reported list of edges differ from actual.`，意味着你确定的道路与实际情况不符。 - `Wrong Answer: get_distance() arguments out of range.`，意味着你在询问时提供了无效的路口编号作为参数。 - `Wrong Answer: Too many calls to get_distance().`，意味着你超出了最大询问次数限制。 - 包含两行信息，分别是 `Score: s%` 和 `Correct: x out of y queries used.`，意味着你获得了该测试点 $s\%$ 的分数，最大询问次数为 $y$ 次，你使用了其中的 $x$ 次。

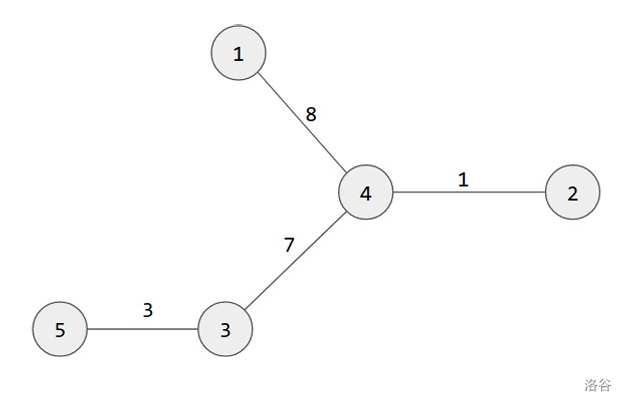
### 调用示例 我们考虑如下的城市地图，展示一种可能的函数调用过程。  假设此时最大询问次数 $Q=5\times 10^5$。 你的函数将这样被调用恰好一次： ```cpp find_roads(5, 500000, A, B, W); ``` 其中 $A,B,W$ 是定义在测试程序中的数组。 一种可能的交互过程如下： - `get_distance(5, 4) = 10`：`get_distance` 函数返回从路口 $5$ 到达路口 $4$ 的最少分钟数。路线 $5\to 3\to 4$ 是最短的，需要 $10$ 分钟。 - `get_distance(2, 4) = 1`：`get_distance` 函数返回了从路口 $2$ 到达路口 $4$ 的最少分钟数。直接从 $2$ 走到 $4$ 是最短的，需要 $1$ 分钟。 - `get_distance(1, 3) = 15`：`get_distance` 函数返回了从路口 $1$ 到达路口 $3$ 的最少分钟数。路线 $1\to 4\to 3$ 是最短的，需要 $15$ 分钟。 - `get_distance(1, 2) = 9`：`get_distance` 函数返回了从路口 $1$ 到达路口 $2$ 的最少分钟数。路线 $1\to 4\to 2$ 是最短的，需要 $9$ 分钟。 此时，我们假设你的 `find_roads` 函数认为自己已经掌握了足够的信息，可以推导出正确的地图，所以将 $A,B,W$ 数组分别赋值为 $A=[3,4,4,5],B=[4,1,2,3],W=[7,8,1,3]$，然后终止。 这只是一种可能的答案，因为返回道路的顺序可以是任意的，同一道路端点的顺序也可以是任意的。 ### 子任务 对于 $100\%$ 的数据，$2\le N\le1000$，$1\le A_i,B_i\le N$，$1\le W_i\le 10^9$。 | 子任务 | 得分 | $Q$ | 特殊性质及备注 | | :----------: | :----------: | :----------: | :----------: | | $1$ | $9$ | $=5\times 10^5$ | $W_i=1$ | | $2$ | $16$ | $=5\times 10^5$ | 无特殊限制 | | $3$ | $13$ | $=12000$ | 每个路口最多连接两条道路，且 $W_i=1$ | | $4$ | $19$ | $=12000$ | 每个路口最多连接两条道路 | | $5$ | $43$ | $=25000$ | 无特殊限制，但有特殊的计分规则（请参阅**计分细则**） | ### 计分细则 子任务 $5$ 适用于以下的计分规则。你的得分依赖于你实现的函数询问的次数 $q$。 - 如果 $q>25000$，你将获得 $0$ 分。 - 如果 $12000