P11598 [NOISG 2018 Finals] Safety

译自 [NOISG 2018 Finals E. Safety](https://github.com/noisg/sg_noi_archive/tree/master/2018/tasks/safety)。

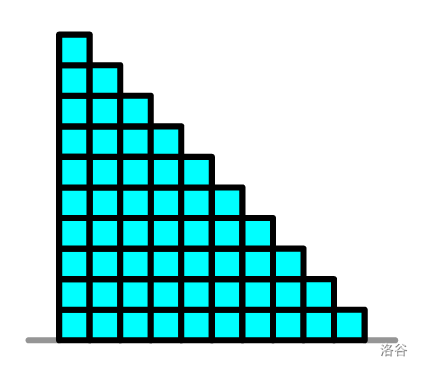
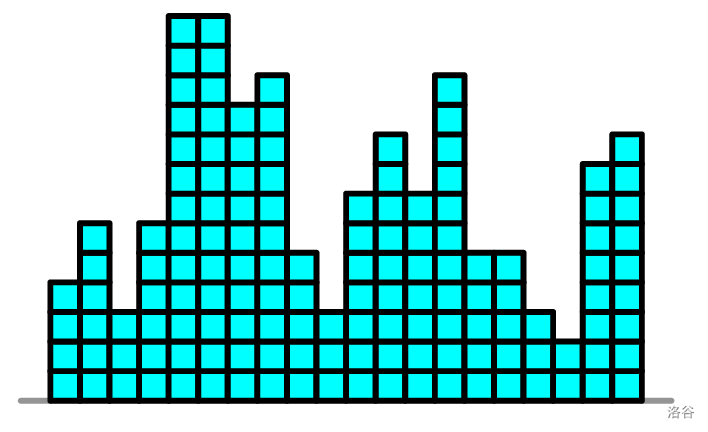
小老鼠 Squeaky 最近开始欣赏视觉艺术，并尝试创作自己的艺术作品，在城里最负盛名的艺术节上展出！ 他的作品由若干发光柱组成，其中每个发光柱又都是由发光立方体堆砌而成的。 具体来说，他的作品是排成一条直线的 $N$ 个发光柱，从左到右编号为 $1$ 到 $N$。其中第 $i$ 个发光柱的高度为 $S_i$，意味着它由 $S_i$ 个发光立方体堆砌而成。 例如下图是 $N=20$ 时一种可能的作品：  然而，观众撞到不安全的展品将造成灾难性的后果。所以，安全委员会要求 Squeaky 保证作品的安全性。具体来说，作品安全当且仅当任意两个相邻发光柱的高度差不超过 $H$，即 $|S_i-S_{i+1}|\le H,\forall i\in[1,N)$。 Squeaky 的作品可能是不安全的，为了确保正常展出，他希望通过修改作品使其安全。 他可以进行的修改只有两种： - 在发光柱 $k$ 上添加一个发光立方体，即 $S_k\gets S_k+1$。 - 从还有至少一个发光立方体的发光柱 $k$ 上移除一个发光立方体，即 $S_k\gets S_k-1$。 注意，即使一个发光柱没有发光立方体，我们也认为它依然存在于原来的位置。 你的任务是帮助 Squeaky 确定至少需要多少次修改他的作品才能安全。

无

无

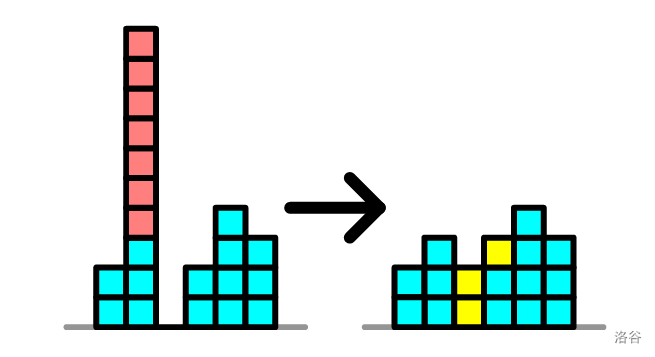
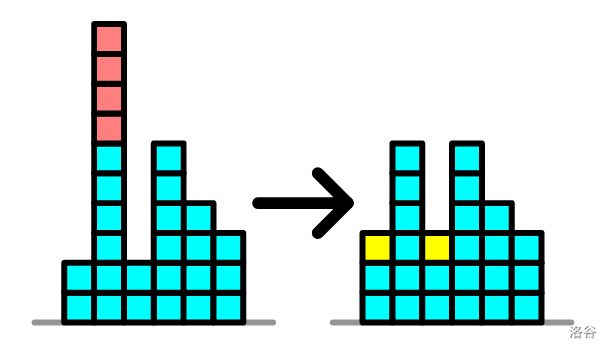
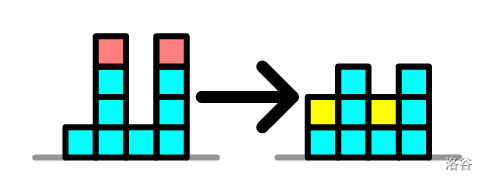
### 样例 #1 解释  如图所示，我们删去红色立方体，添加黄色立方体，通过修改 $10$ 次使 Squeaky 的作品安全：任意相邻的两个发光柱高度差都不超过 $H=1$。 可以证明，不存在少于 $10$ 步的修改方法。 这组样例满足子任务 $3$ 和子任务 $5$ 至 $9$。 ### 样例 #2 解释  如图所示，我们删去红色立方体，添加黄色立方体，通过修改 $6$ 次使 Squeaky 的作品安全。可以证明，不存在少于 $6$ 步的修改方法。 这组样例满足子任务 $5$ 至 $9$。 ### 样例 #3 解释  如图所示，我们删去红色立方体，添加黄色立方体，通过修改 $4$ 次使 Squeaky 的作品安全。可以证明，不存在少于 $4$ 步的修改方法。 这组样例满足子任务 $1$ 至 $3$ 和子任务 $5$ 至 $9$。 ### 样例 #4 解释  Squeaky 的作品本来就是安全的，所以不需要进行修改。 这组样例满足子任务 $3$ 和子任务 $5$ 至 $9$。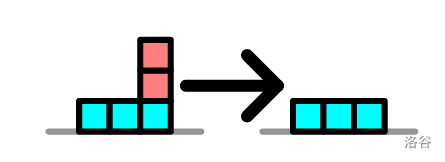 ### 样例 #5 解释  如图所示，我们删去红色立方体，通过修改 $2$ 次使 Squeaky 的作品安全。可以证明，不存在少于 $2$ 步的修改方法。 这组样例满足所有子任务。 ### 子任务 对于 $100\%$ 的数据，$1\le N\le 2\times 10^5$，$0\le H\le 10^9$，$0\le S_i\le 10^9$。 | 子任务 | 得分 | 数据范围及特殊性质 | | :----------: | :----------: | :----------: | | $1$ | $3$ | $N\le 10$，$S_i\le 4$ | | $2$ | $4$ | $N\le 14$，$H\le 1$，$S_i\le 4$ | | $3$ | $9$ | $N\le10$，$H\le 2$ | | $4$ | $5$ | $H=0$ | | $5$ | $6$ | $N\le 500$，$S_i\le 400$ | | $6$ | $11$ | $N\le 500$，$S_i\le 5\times 10^3$ | | $7$ | $11$ | $N\le 5\times 10^3$，$S_i\le 5\times 10^3$ | | $8$ | $22$ | $N\le 5\times 10^3$ | | $9$ | $29$ | 无特殊限制 |