P11640 Graph

**hack 数据已添加，位于 Subtask#5，不计分。**

有一张 $n$ 个点的图，每个点可以是**黑色**或**白色**的。 有 $m$ 条限制，第 $i$ 条限制会给定 $a_i,b_i,c_i$，表示 $a_i\Rightarrow b_i$ 需要有一条长度为 $c_i$ 的路径，路径可以重复经过某条边或点。 问是否存在一个若干条边权为 $1$ 有向边的图，满足： - 满足上述 $m$ 个条件。 - 假如这张图有 $k$ 条边，则对于每个 $\forall 1\le i\le k$，设第 $i$ 条边是由 $u_i$ 指向 $v_i$ 的，那么 $u_i$ 的颜色与 $v_i$ 的不同。

第一行一个整数 $T$，表示数据的组数。 对于每组数据，第一行两个整数 $n,m$。 接下来 $m$ 行，每行三个整数，分别为 $a_i,b_i,c_i$。

$T$ 行，每行一个字符串 $s\in\{\tt{Yes},\tt{No}\}$。 第 $i$ 行表示第 $i$ 个问题的答案。

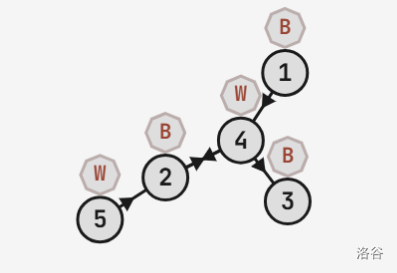
**【样例解释】** 可以构造出  以满足要求。 ------------ **【数据范围】** **本题采用捆绑测试。** - Subtask #1（$5\text{pts}$）：$m=0$。 - Subtask #2（$20\text{pts}$）：$n\le 10$。 - Subtask #3（$25\text{pts}$）：$n\le 10^3$。 - Subtask #4（$50\text{pts}$）：无特殊限制。 对于 $100\%$ 的数据，$1\le T\le 10$，$1\le n\le 10^6$，$0\le m\le 10^6$，$1\le a_i,b_i\le n$，$0\le c_i\le 10^9$。