P11704 [ROIR 2025] 旅行路线

翻译自 [ROIR 2025 D2T4](https://neerc.ifmo.ru/school/archive/2024-2025/ru-olymp-regional-2025-day2.pdf)。

一群学生来到一座新城市游览，决定参观这里的名胜古迹。这座城市可以看作一个 $n \times m$ 的矩形网格，其中某些格子上有景点。 他们从格子 $(1, 1)$ 开始旅程，想要先到达格子 $(n, m)$，然后再返回起点。此外，城市中有 $k$ 个景点，位于格子 $(x_1, y_1), \dots, (x_k, y_k)$，他们一定要全部参观到。  他们可以花费一分钟从格子 $(a, b)$ 移动到与之相邻（即满足 $|a - c| + |b - d| = 1$）的格子 $(c, d)$。显然，完成整个路线至少需要 $2n + 2m - 4$ 分钟。 我们称一条路线为“有趣的”，如果它满足以下条件： - 完成该路线所需的时间恰好是 $2n + 2m - 4$ 分钟； - 路线中的每个格子最多经过一次； - 路线必须经过所有包含景点的格子。 请帮助他们计算一共有多少条不同的有趣的路线。由于结果可能很大，只需要输出其对 $10^9 + 7$ 取模的结果。

第一行输入三个整数 $n$，$m$ 和 $k$（$3 \leq n, m \leq 10^6$，$0 \leq k \leq 2000$）。 接下来 $k$ 行，每行包含两个整数 $x_i$ 和 $y_i$（$1 \leq x_i \leq n$，$1 \leq y_i \leq m$）。保证所有的 $(x_i, y_i)$ 都是不同的，即 $\forall (i, j), x_i \neq x_j \vee y_i \neq y_j$。

输出一个整数，表示有趣的路线的数量对 $10^9 + 7$ 取模的结果。

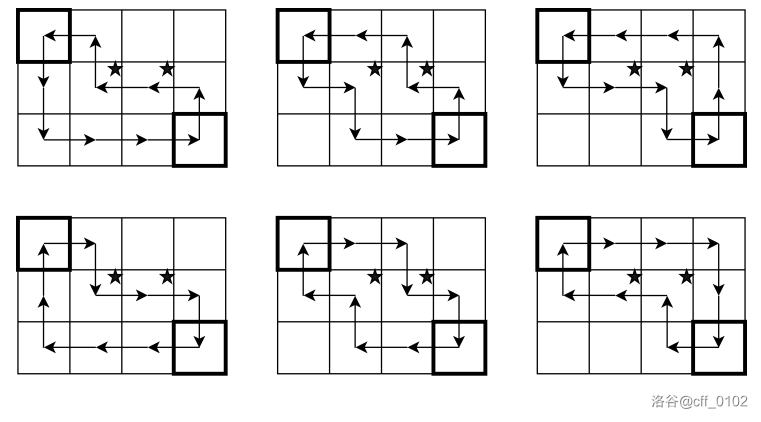
下图展示了样例一中所有有趣的路线，其中带有星号的格子存在名胜古迹。  本题使用 Subtask 捆绑测试。数据中 Subtask 0 是样例。 |子任务|分数|特殊性质| |:-:|:-:|:-:| |$1$|$5$|$n=3$，$m, k \leq 100$| |$2$|$9$|$n, m, k \leq 5$| |$3$|$6$|$n, m, k \leq 8$| |$4$|$17$|$n, m, k \leq 30$| |$5$|$16$|$n, m, k \leq 100$| |$6$|$8$|$k=0$| |$7$|$11$|$k=1$| |$8$|$12$|$k \leq 16$| |$9$|$9$|$k \leq 100$| |$10$|$7$|无|$