P11706 「KTSC 2020 R1」穿越

**请使用 C++17 或 C++20 提交本题** 你需要在程序开头加入如下代码： ```cpp #include void init(int N, int M, std::vector Y1, std::vector Y2); long long minimize(int A, int B); ``` 题目译自 [2020년도 국제정보올림피아드 대표학생 선발고사 - 1차 선발고사](https://www.ioikorea.kr/archives/ioitst/2020/) T2「 [뚫기](https://assets.ioikorea.kr/ioitst/2020/1/breakthru/breakthru_statement.pdf)」

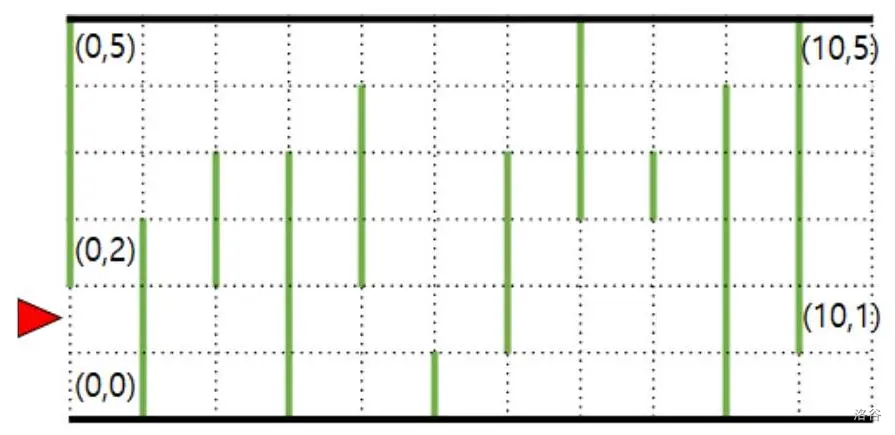
在不久的将来，新加坡流行一种叫做「穿越」的游戏。游戏规则很简单：玩家需要控制一个楔形飞船从左到右穿过一个 $N \times M$ 的隧道。隧道中有 $N$ 个绿色障碍物阻挡飞船前进。障碍物位于每个格子的左侧墙壁上，跨越多个格子的连续障碍物被视为一个障碍物。为了方便描述，飞船前进的方向为 $x$ 轴，与之垂直的方向为 $y$ 轴。在相同的 $x$ 坐标上只能有一个障碍物。 例如，下图展示了一个 $11 \times 6$ 的隧道，其中有 $11$ 个障碍物。最左边的障碍物从 $(0,2)$ 到 $(0,5)$，最右边的障碍物从 $(10,1)$ 到 $(10,5)$。  飞船在每个格子中可以进行两种移动之一。第一种移动是瞬移。瞬移是将飞船从当前格子移动到相同 $x$ 坐标的任意格子。无论移动到哪个格子，瞬移的费用始终为 $A$。例如，下图展示了飞船从 $(0,1)$ 瞬移到 $(0,5)$ 的情况，费用为 $A$。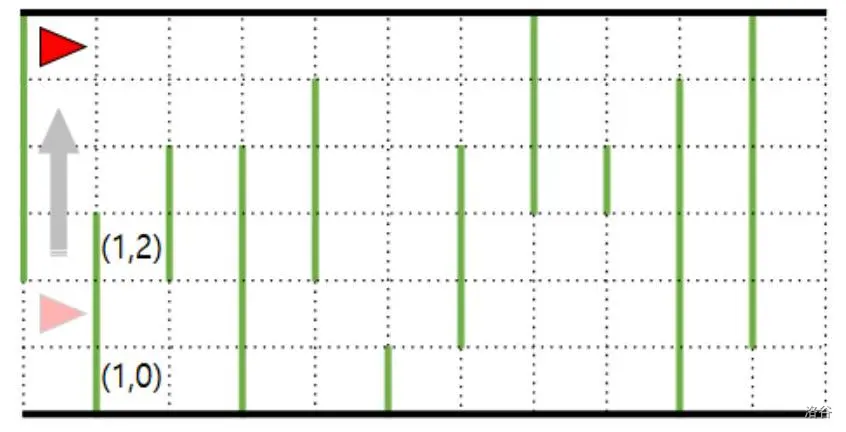  飞船的第二种移动是前进，费用为 $0$。即使前进方向上有障碍物，飞船也可以穿过障碍物，但这会产生费用 $B$。例如，下图展示了飞船从 $(6,5)$ 前进到 $(7,5)$ 的情况，由于 $(7,5)$ 有障碍物，费用为 $B$。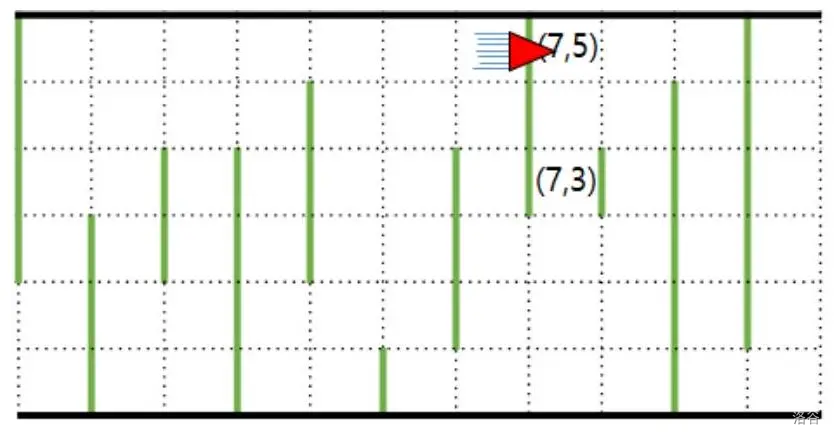  当飞船完全穿过隧道时，游戏结束。游戏得分是飞船穿过隧道时产生的总费用。显然，得分越低越好。游戏开始时，玩家可以选择飞船的初始 $y$ 坐标，且不产生费用。游戏结束时，飞船的 $y$ 坐标无关紧要。 即使隧道的大小和障碍物的位置相同，费用 $A$ 和 $B$ 的变化也会影响游戏得分和飞船的最佳移动策略。你需要实现以下两个函数，利用给定的隧道大小和障碍物位置，在每次费用 $A$ 和 $B$ 变化时，计算可能的最低游戏得分。 ``` void init(int N, int M, int Y1[], int Y2[]); ``` - 该函数在程序开始时调用一次。 - 参数 $N$ 和 $M$ 表示隧道的大小 $N \times M$。 - 参数 $Y1$ 和 $Y2$ 是表示障碍物位置的数组，长度为 $N$。如果从 $(X, Y_1[X])$ 到 $(X, Y_2[X])$ 有一个障碍物，则 $Y1[X]$ 和 $Y2[X]$ 分别表示 $Y_1$ 和 $Y_2$。 ``` long long minimize(int A, int B); ``` - 参数 $A$ 是飞船瞬移一次的费用，$B$ 是飞船穿过一次障碍物的费用。该函数返回飞船穿过隧道所需的最小费用。 你需要提交一个代码，该代码中实现以下函数： ``` void init(int N, int M, int Y1[], int Y2[]); long long minimize(int A, int B); ``` 这些函数应按照上述描述工作。当然，你可以创建其他函数并在内部使用。提交的代码不应执行输入输出操作或访问其他文件。

示例评测程序按以下格式读取输入： - 第 $1$ 行：$N\,M\,Q$（$N \times M$：隧道的大小，$Q$：查询的数量） - 第 $2+i\ (0 \leq i \leq N-1)$ 行：$Y_1\,Y_2$（$x$ 坐标为 $i$ 的障碍物的 $y$ 坐标位置从 $Y_1$ 到 $Y_2$） - 第 $2+N+i\ (0 \leq i \leq Q-1)$ 行：$A\,B$（$A$：瞬移费用，$B$：穿过障碍物的费用）

示例评测程序对每个查询调用你的代码中的 `minimize()` 函数，并输出返回值。

### 样例说明 #1 | 函数调用 | 返回值 | | :----------: | :----------: | |`init(3, 5, {2, 0, 1}, {4, 2, 3})`|| |`minimize(2, 1)`|$1$| |`minimize(3, 5)`|$3$| ### 数据范围 对于所有输入数据，满足： - $1 \leq N \leq 10^4$ - $1 \leq M \leq 10^{9}$ - $1 \leq Q \leq 10^{6}$ - $0 \leq Y_1 \leq Y_2 \leq M-1$ - $0 \leq A, B \leq 10^{9}$ 详细子任务附加限制及分值如下表所示。 | 子任务编号 | 分值 | 子任务附加限制 | | :----------: | :----------: | :----------: | |$1$|$7$|$Q=1, N \leq 3,000, M \leq 3,000$| |$2$|$22$|$Q \leq 50$| |$3$|$19$|$N \leq 500$| |$4$|$21$|$N \leq 2,500$| |$5$|$31$|无附加限制|