P11712 「KTSC 2020 R2」冰战

**请使用 C++17 或 C++20 提交本题** 你需要在程序开头加入如下代码： ```cpp #include void maximize(std::vector A); ``` 题目译自 [2020년도 국제정보올림피아드 대표학생 선발고사 - 2차 선발고사](https://www.ioikorea.kr/archives/ioitst/2020/) T4「 [아이싱](https://assets.ioikorea.kr/ioitst/2020/1/ising/ising_statement.pdf)」

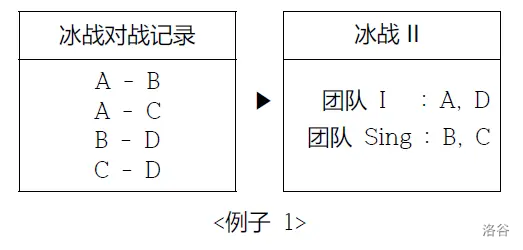
冰战是一款在中学生和高中生中非常流行的在线一对一对战游戏。游戏公司决定扩展这款游戏，开发了冰战 II，这是一款专为团队对战设计的游戏，允许团队 I 和团队 Sing 之间进行对战。冰战 II 利用玩家在冰战中的对战记录，以独特的方式组建团队。具体来说，在冰战中进行过一对一对战的两个玩家必须分属不同的团队。每个团队至少有一名成员，两个团队的人数可以不同。 例如，下表展示了四名玩家 $A$、$B$、$C$、$D$ 在冰战中的对战记录，以及在冰战 II 中的团队组成。  然而，冰战 II 服务器将在 $3$ 分钟后开放，但发现了一个致命问题。例如，如果玩家 $A$、$B$、$C$ 都曾互相对战过，他们必须分别加入不同的团队，这使得无法组成团队 I 和团队 Sing。 为了解决这个问题，我们决定删除最少数量的对战记录。例如，考虑下图中四名玩家 $A$、$B$、$C$、$D$ 的冰战对战记录（左图）。在这种情况下，至少需要删除一条记录，如果删除 $A-B$（中图），则可以组成两个团队（右图）。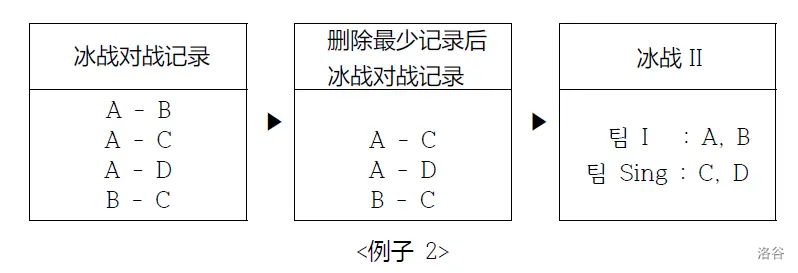  另一个例子，考虑以下冰战对战记录。在这种情况下，至少需要删除两条对战记录，如果删除 $A-B$ 和 $C-D$，则可以组成两个团队。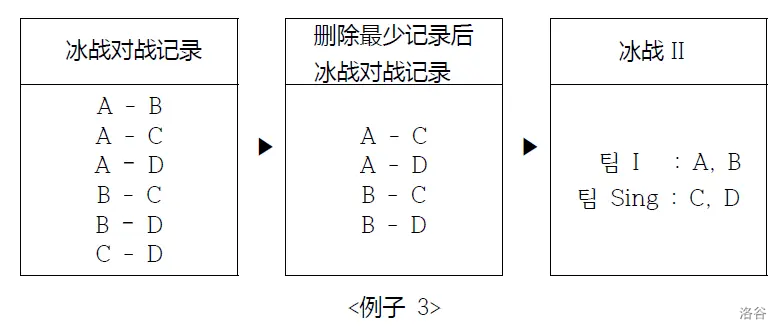  但是，游戏将在 $3$ 分钟后上线，因此最多只能删除两条记录。如果需要删除三条或更多记录，可能需要推迟上线。 在这种情况下，游戏公司想知道有多少种不同的方法可以删除最少数量的对战记录，以便组成两个团队。也就是说，当需要删除的最少对战记录数量为 $K$ 时，计算大小为 $K$ 的可删除对战记录子集的数量。 在样例 2 中，删除 $\{A-B\}, \{A-C\}$ 或 $\{B-C\}$ 都可以组成两个团队，因此答案是 $3$。在样例 3 中，删除 $\{A-B, C-D\}, \{A-C, B-D\}$ 或 $\{A-D, B-C\}$ 都可以组成两个团队，因此答案是 $3$。 你需要实现以下函数，利用给定的冰战对战记录，计算有多少种不同的方法可以删除最少数量的对战记录，以便组成两个团队。在这种情况下，删除对战记录的顺序不重要。如果无法通过删除两条或更少的记录来进行游戏，则返回 `0`。如果不需要删除任何记录，则返回 `1`，因为这是最快的唯一方法。 `long long count_ways(int N, vector U, vector V);` - 参数 `N` 是玩家数量，`U` 和 `V` 是大小为 $M$ 的 `vector`，表示玩家 $U_{i}$ 和 $V_{i}$ 之间有冰战对战记录。函数返回删除最少数量的对战记录以组成两个团队的不同方法的数量。如果需要删除三条或更多记录，则返回 `0`。 该函数应按照上述描述工作。当然，你可以创建其他函数并在内部使用。提交的代码不应执行输入输出操作或访问其他文件。

示例评测程序按以下格式读取输入： - 第 $1$ 行：$N\,M$，$N$ 表示玩家数量，$M$ 表示冰战对战记录数量 - 第 $2+i (0 \leq i \leq M-1)$ 行：$U_{i}\,V_{i}$（玩家 $U_{i}$ 和玩家 $V_{i}$ 之间的冰战对战记录）

示例评测程序将输出你的代码中 `count_ways()` 函数返回的值。

### 样例说明 #1 以下是样例 1 中函数调用及其返回值： | 调用函数 | 返回值 | | :----------: | :----------: | |`count(4, {1,1,2,3}, {2,3,4,4})`|`1`| ### 数据范围 对于所有输入数据，满足： - $3 \leq N \leq 2.5\times 10^5$ - $N-1 \leq M \leq 2.5\times 10^5$ - $1 \leq U_{i}, V_{i} \leq N (0 \leq i \leq M-1)$ - $U_{i} \neq V_{i}$ - $U_{i}=U_{j}$ 且 $V_{i}=V_{j}$ 时 $i=j$ - 任何两个玩家通过对战记录直接或间接相关 详细子任务附加限制及分值如下表所示。 | Subtask | 分值 | 约束 | | :----------: | :----------: | :----------: | |$1$|$10$|$N \leq 200, M \leq 200$| |$2$|$23$|$N \leq 5000, M \leq 5000$| |$3$|$11$|$N \leq 500$| |$4$|$25$|$N \leq 5000$| |$5$|$31$|$M-N \leq 200$| |$6$|$50$|无附加限制| 本题满分为 $150$ 分。