P11774 [COTS 2013] 矩形覆盖 / BAKTERIJE
题目描述
在平面直角坐标系上有 $N$ 个边与坐标轴平行,且互不重叠的矩形,给定它们的左下角坐标 $(x_1,y_1)$ 和右上角坐标 $(x_2,y_2)$。
你现在有一个长为 $W$,宽为 $H$ 的矩形 $S$,你需要选择一个位置放置这个矩形,使得原坐标系上的矩形和 $S$ 有交的矩形的数量尽可能多。
注意:
- 矩形 $S$ 顶点不必放置在整数坐标上(见样例 $1$ 图片)。
- 有交指两个矩形重叠位置的面积 $>0$。
输入格式
第一行两个整数 $W,H$,表示 $S$ 的长宽。
第二行一个整数 $N$,表示矩形数量。
以下 $N$ 行,每行四个整数 $x_1,y_1,x_2,y_2$,表示每个矩形的左下角和右上角坐标。
输出格式
一行一个整数,即和 $S$ 有交的矩形的最多的数量。
说明/提示
【样例解释】
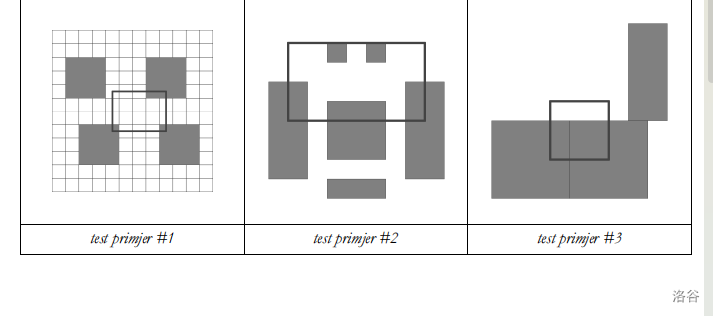
【数据范围与约定】
- 对于 $30 \%$ 的数据,满足 $N\le 30$。
- 对于 $60 \%$ 的数据,满足 $N\le 1000$。
- 对于 $100 \%$ 的数据,满足 $1 \le N \le 100000,1\le W,H \le 50000,0 \le x_1