P11803 【MX-X9-T7】『GROI-R3』此花绽放之时

在盛开的樱花树下， 属于我们的最后一场演奏会开始了。

樱乃给你一棵 $n$ 个点的树，点的编号为 $1\sim n$。每个点初始有点权 $a_i=0$ 和颜色 $c_i$。你需要维护三种操作： - `1 x y c`：把点 $x\sim y$ 最短路径上所有点颜色改为 $c$。 - `2 x w`：把点 $x$ 所属极大相同颜色连通块中的所有点的点权增加 $w$。 - `3 x`：查询点 $x$ 点权。

第一行，两个正整数表示 $n, q$，其中 $q$ 表示操作总数。 第二行，$n$ 个正整数 $c_1,\ldots,c_n$。 第三行，$n-1$ 个正整数 $f_2,\ldots,f_n$，表示存在边 $(f_i,i)$。保证 $f_i \le i - 1$。 接下来 $q$ 行，每行若干个正整数，表示一次操作，格式见题目描述。

对每个查询操作，输出一行，一个整数，表示答案。

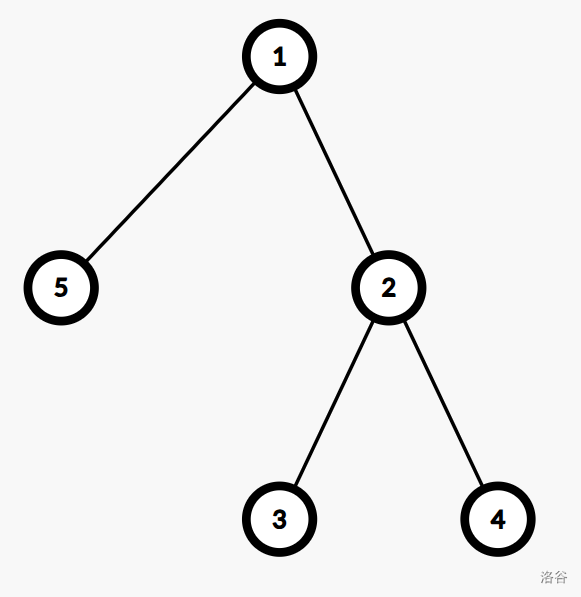
**【样例解释】**  样例的树如图。 一开始所有点颜色均为 $1$。 - 第 $1$ 次操作：询问 $1$ 的点权。答案为 $0$； - 第 $2$ 次操作：把 $1$ 所处极大连通块所有点点权加 $1$。当前点权序列为 $[1,1,1,1,1]$； - 第 $3$ 次操作：查询 $2$ 的点权。答案为 $1$； - 第 $4$ 次操作：把 $3\sim 5$ 最短路径所有点颜色改为 $2$。当前颜色序列为 $[2,2,2,1,2]$； - 第 $5$ 次操作：把 $1$ 所处极大连通块所有点点权加 $2$。当前点权序列为 $[3,3,3,1,3]$； - 第 $6$ 次操作：查询 $1$ 的点权。答案为 $3$； - 第 $7$ 次操作：查询 $4$ 的点权。答案为 $1$。 **【数据范围】** **本题采用捆绑测试。** | 子任务编号 | $n,q\leq$ | 特殊性质 | 分值 | | :----------: | :--: | :------------: | :------: | | 1 | $5000$ | | $10$ | | 2 | $2\times 10^5$ | A | $20$ | | 3 | $2\times 10^5$ | B | $10$ | | 4 | $5\times 10^4$ | | $30$ | | 5 | $2\times 10^5$ | | $30$ | - 特殊性质 A：保证 $f_i=i-1$。 - 特殊性质 B：保证没有 1 操作。 对于 $100\%$ 的数据，保证 $2\leq n,q\leq 2\times 10^5$，$1\leq c_i\leq n$，$1\leq f_i\leq i-1$，$1 \le x, y, c \le n$，$1 \le w \le 10^9$，保证至少有一次 3 操作。