P11825 [TOIP2024] 6174

公元 $1955$ 年，数学家卡布列克(D. R. Kaprekar)发现了以下有趣的性质： 对于所有位数不完全相同的 $4$ 位正整数，将其所有位数依数值由大至小排列所得到的数字减去由小至大排列所得到的数字，如此一来会得到另外一新的 $4$ 位正整数（包含前导零）。若重复上述步骤若干次，必定可以得到 $6174$ 这个数字。又因为以 $6174$ 重复上述步骤计算将会得到 $6174$ 自身，该性质如同黑洞一般只进不出，故 $6174$ 因此而得名「黑洞数」。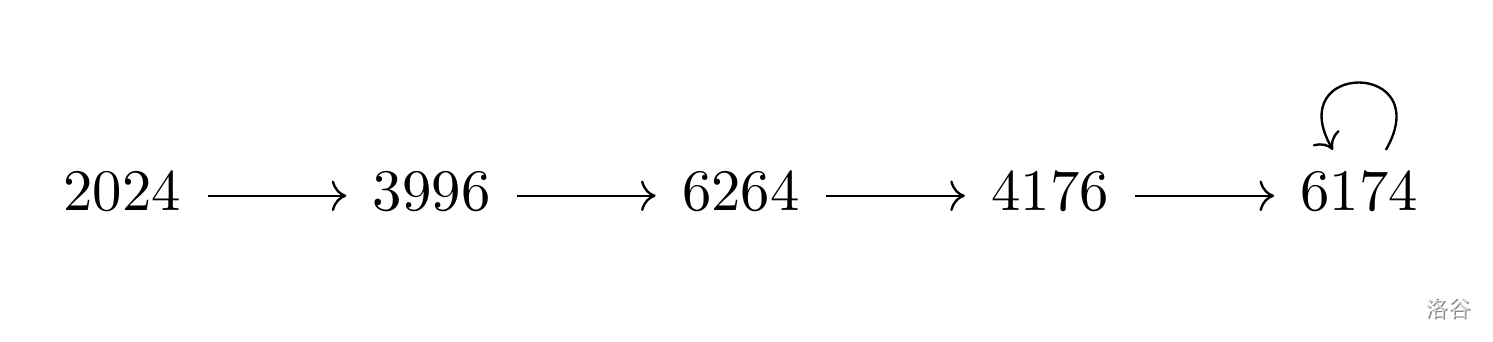 举例来说： $\newline \qquad 2024 \longrightarrow 4220 - 0224 = 3996 \newline \qquad 3996 \longrightarrow 9963 - 3699 = 6264 \newline \qquad 6264 \longrightarrow 6642 - 2466 = 4176 \newline \qquad 4176 \longrightarrow 7641 - 1467 = 6174 \newline \qquad 6174 \longrightarrow 7641 - 1467 = 6174$ 可得：  针对所有位数不完全相同的 $d$ 位数，也有类似的情况，只是最后不一定会停在单一一个数字，而是有可能在一群数字之间循环。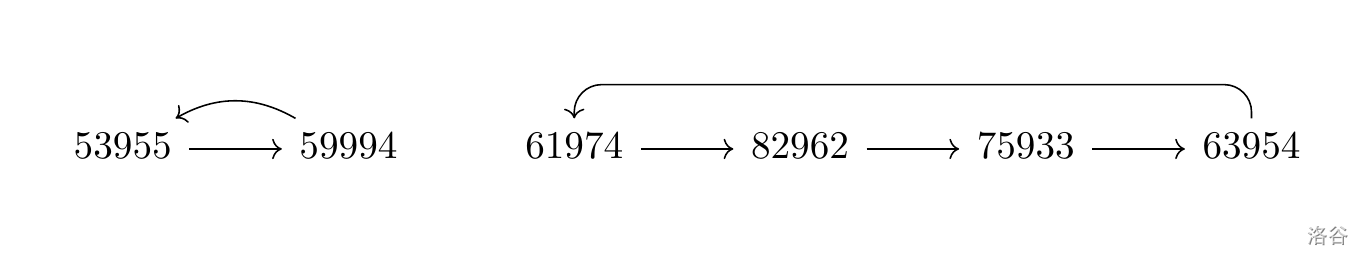例如当 $d = 5$ 时，以下是某两种循环的情形：  不难推论，不论 $d$ 为何，由任一数字开始必定会进入某些数字组成的循环之中（单一数字亦算作循环）。今给定 $n$ 个所有位数不完全相同的 $d$ 位数，请各自输出由该数字作为起始数字进行若干步骤计算后，进入循环时**第一个**遇到的数字。 举例来说，若以 $50985$ 作为起始数字进行若干步骤计算后可以得到如下的结果，可以发现在经过 $7$ 次步骤之后，会得到于先前计算中已经出现过的 $75933$，之后再继续计算将会进入循环之中，而 $75933$ 即为进入循环时**第一个**遇到的数字，故以本例子来说须输出 $75933$。 

> $n$ $d$ > $s_1$ > $s_2$ > $\vdots$ > $s_n$ * $n$ 为一正整数，代表接下来欲询问 $n$ 个数字。 * $d$ 为一正整数，代表接下来欲询问的数字皆为 $d$ 位数。 * $s_i$ 为一正整数，代表第 $i$ 个询问的起始数字（不含前导零）。

> $c_1$ > $c_2$ > $\vdots$ > $c_n$ * $c_i$ 为一正整数，代表以数字 $s_i$ 作为起始数字进行若干步骤计算后，进入循环时**第一个**遇到的数字（不含前导零）。

### 测试数据限制 * $2 \le d \le 10$。 * $1 \le n \le 10^4$。 * $1 \le s_i < 10^d$。 * 所有输入的数均为正整数。 * 保证 $s_i$ 在 $d$ 位数表示中所有位数不完全相同。 * 保证 $n$ 个数字进行若干步骤计算，进入循环时其总计算步骤数不超过 $10^5$。 ### 评分说明 本题共有三组子任务，条件限制如下所示。 每一组可有一或多笔测试数据，该组所有测试数据皆需答对才会获得该组分数。 | 子任务 | 分数 | 额外输入限制 | | :------: | :----: | ------------ | | 1 | $12$ | 输入满足 $d = 3$ 或 $d = 4$。 | | 2 | $24$ | 输入满足 $2 \le d \le 6$ 且 $1 \le n \le 100$。 | | 3 | $64$ | 无额外限制。 |