P11825 [TOIP2024] 6174

西元 $1955$ 年，數學家卡布列克(D. R. Kaprekar)發現了以下有趣的性質： 對於所有位數不完全相同的 $4$ 位數正整數，將其所有位數依數值由大至小排列所得到的數字減去由小至大排列所得到的數字，如此一來會得到另外一新的 $4$ 位數正整數（包含前導零）。若重複上述步驟若干次，必定可以得到 $6174$ 這個數字。又因為以 $6174$ 重複上述步驟計算將會得到 $6174$ 自身，該性質如同黑洞一般只進不出，故 $6174$ 因此而得名「黑洞數」。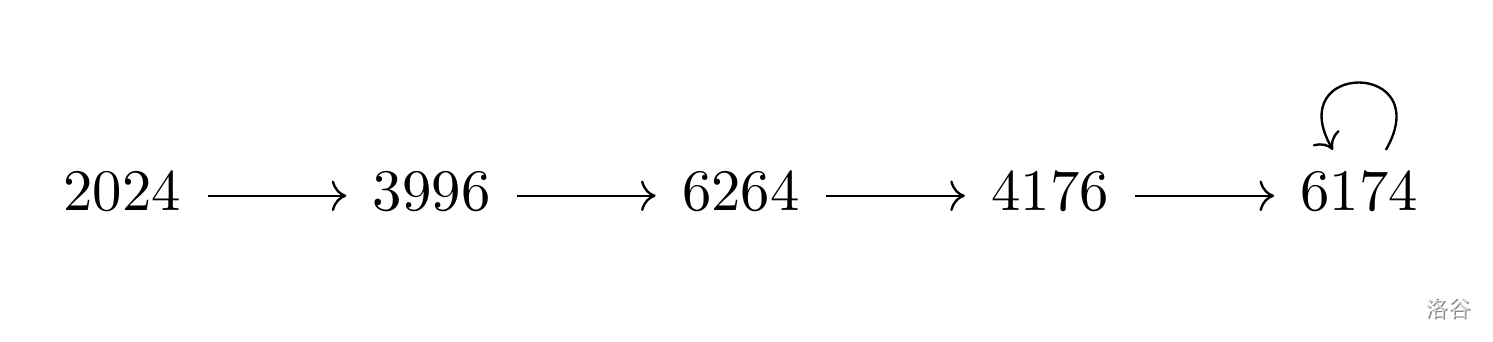 舉例來說： $\newline \qquad 2024 \longrightarrow 4220 - 0224 = 3996 \newline \qquad 3996 \longrightarrow 9963 - 3699 = 6264 \newline \qquad 6264 \longrightarrow 6642 - 2466 = 4176 \newline \qquad 4176 \longrightarrow 7641 - 1467 = 6174 \newline \qquad 6174 \longrightarrow 7641 - 1467 = 6174$ 可得：  針對所有位數不完全相同的 $d$ 位數，也有類似的情況，只是最後不一定會停在單一一個數字，而是有可能在一群數字之間循環。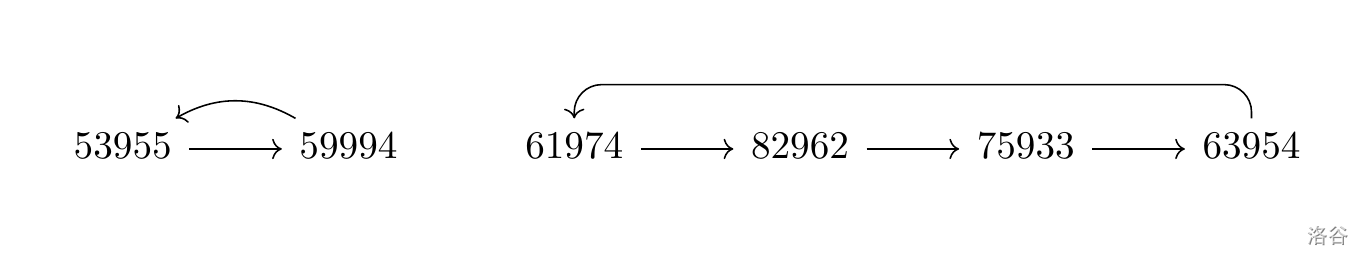例如當 $d = 5$ 時，以下是某兩種循環的情形：  不難推論，不論 $d$ 為何，由任一數字開始必定會進入某些數字組成的循環之中（單一數字亦算作循環）。今給定 $n$ 個所有位數不完全相同的 $d$ 位數，請各自輸出由該數字作為起始數字進行若干步驟計算後，進入循環時**第一個**遇到的數字。 舉例來說，若以 $50985$ 作為起始數字進行若干步驟計算後可以得到如下的結果，可以發現到在經過 $7$ 次步驟之後，會得到於先前計算中已經出現過的 $75933$，之後再進行計算將會進入循環之中，而 $75933$ 即為進入循環時**第一個**遇到的數字，故以本例子來說須輸出 $75933$。 

> $n$ $d$ > $s_1$ > $s_2$ > $\vdots$ > $s_n$ * $n$ 為一正整數，代表接下來欲詢問 $n$ 個數字。 * $d$ 為一正整數，代表接下來欲詢問的數字皆為 $d$ 位數。 * $s_i$ 為一正整數，代表第 $i$ 個詢問的起始數字（不含前導零）。

> $c_1$ > $c_2$ > $\vdots$ > $c_n$ * $c_i$ 為一正整數，代表以數字 $s_i$ 作為起始數字進行若干步驟計算後，進入循環時**第一個**遇到的數字（不含前導零）。

### 測資限制 * $2 \le d \le 10$。 * $1 \le n \le 10^4$。 * $1 \le s_i < 10^d$。 * 所有輸入的數皆為正整數。 * 保證 $s_i$ 在 $d$ 位數表示中所有位數不完全相同。 * 保證 $n$ 個數字進行若干步驟計算，進入循環時其總計算步驟數不超過 $10^5$。 ### 評分說明 本題共有三組子任務，條件限制如下所示。 每一組可有一或多筆測試資料，該組所有測試資料皆需答對才會獲得該組分數。 | 子任務 | 分數 | 額外輸入限制 | | :------: | :----: | ------------ | | 1 | $12$ | 輸入滿足 $d = 3$ 或 $d = 4$。 | | 2 | $24$ | 輸入滿足 $2 \le d \le 6$ 且 $1 \le n \le 100$。 | | 3 | $64$ | 無額外限制。 |