P11826 [TOIP2024] 奇巧方块

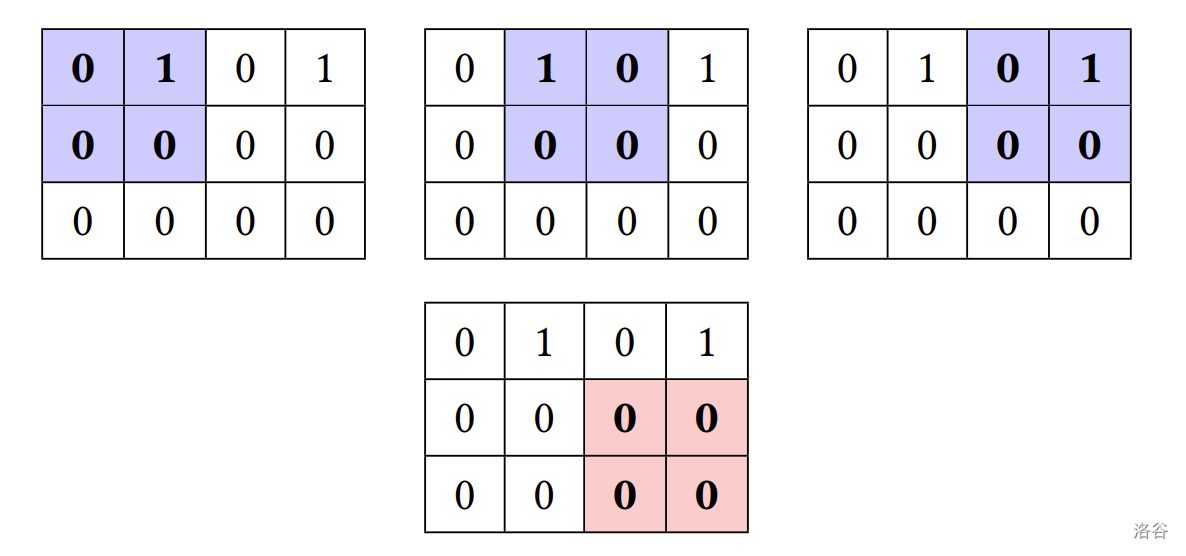
有一个 $m$ 列 $n$ 行 的 $01$-矩阵恰有 $t$ 个 $1$，且所有的 $1$ 皆位于同一列。$1$ 所在的列编号为 $r$，行编号为 $c_1, c_2, \ldots, c_t$。请计算共有几个 $k\times k$ 的子矩阵包含奇数个 $0$。 以下图中 $3\times 4$ 的 $01$-矩阵为例，共有 $3$ 个 $2\times 2$ 的子矩阵包含奇数个 $0$，如蓝色的子矩阵所标示。红色的 $2\times 2$ 的子矩阵包含 $4$ 个 $0$，故不列入计算。 

> $m$ $n$ > $t$ $k$ $r$ > $c_1$ $c_2$ $\cdots$ $c_t$ * $m, n$ 分别为矩阵之列数与行数。 * $t$ 为 $1$ 的个数。 * $k$ 为子矩阵的大小。 * $r$ 为 $t$ 个 $1$ 所在之列的编号。 * $c_1, c_2, \ldots, c_t$ 为 $1$ 的行的编号，且保证 $c_i < c_{i+1}$。

> $x$ 一个整数 $x$，为含奇数个 $0$ 的 $k\times k$ 子矩阵个数。

### 测试数据限制 * $1 \le m, n\le 10^9$。 * $0 \le t \le \min(n, 10^5)$。 * $1 \le k \le \min(m, n)$。 * $1 \le r \le m$。 * $1 \le c_i \le n$。 * 输入的数均为整数。 ### 评分说明 本题共有三组子任务，条件限制如下所示。 每一组可有一或多个测试数据，该组所有测试数据皆需答对才会获得该组分数。 | 子任务 | 分数 | 额外输入限制 | | :------: | :----: | ------------ | | 1 | $11$ | 输入满足 $m, n \le 1000$。 | | 2 | $41$ | 输入满足 $m, n \le 10^5$。 | | 3 | $48$ | 无额外限制。 |