P11826 [TOIP2024] 奇巧方塊

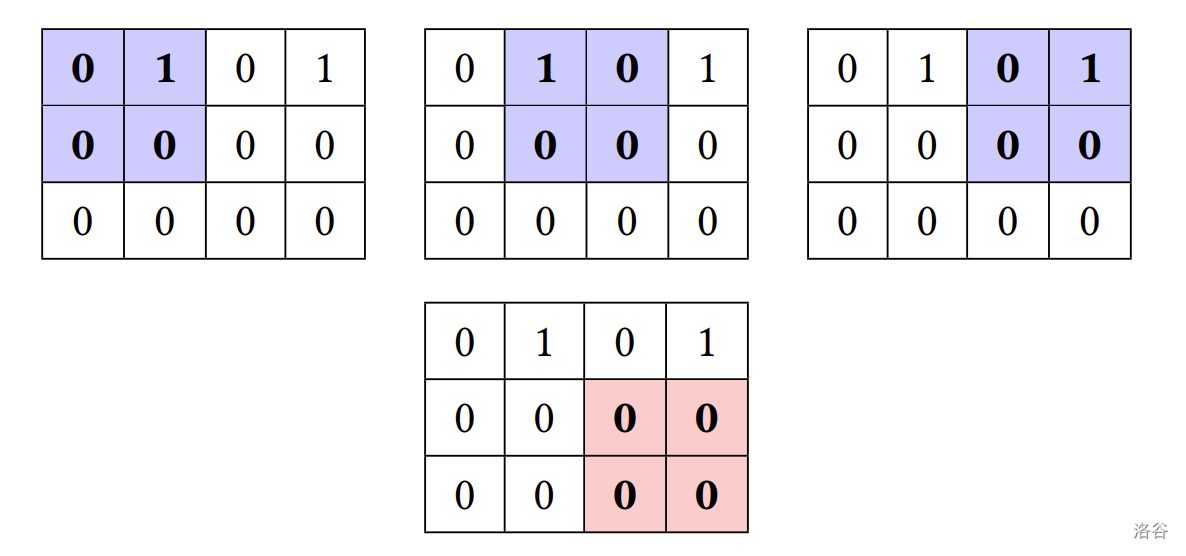
有一個 $m$ 列 $n$ 行 的 $01$-矩陣恰有 $t$ 個 $1$，且所有的 $1$ 皆位於同一列。$1$ 所在的列編號為 $r$，行編號為 $c_1, c_2, \ldots, c_t$。請計算共有幾個 $k\times k$ 的子矩陣包含奇數個 $0$。 以下圖中 $3\times 4$ 的 $01$-矩陣為例，共有 $3$ 個 $2\times 2$ 的子矩陣包含奇數個 $0$，如藍色的子矩陣所標示。紅色的 $2\times 2$ 的子矩陣包含 $4$ 個 $0$，故不列入計算。 

> $m$ $n$ > $t$ $k$ $r$ > $c_1$ $c_2$ $\cdots$ $c_t$ > > * $m, n$ 分別為矩陣之列數與行數。 * $t$ 為 $1$ 的個數。 * $k$ 為子矩陣的大小。 * $r$ 為 $t$ 個 $1$ 所在之列的編號。 * $c_1, c_2, \ldots, c_t$ 為 $1$ 的行的編號，且保證 $c_i < c_{i+1}$。

> $x$ 一個整數 $x$，為含奇數個 $0$ 的 $k\times k$ 子矩陣個數。

### 測資限制 * $1 \le m, n\le 10^9$。 * $0 \le t \le \min(n, 10^5)$。 * $1 \le k \le \min(m, n)$。 * $1 \le r \le m$。 * $1 \le c_i \le n$。 * 輸入的數皆為整數。 ### 評分說明 本題共有三組子任務，條件限制如下所示。 每一組可有一或多筆測試資料，該組所有測試資料皆需答對才會獲得該組分數。 | 子任務 | 分數 | 額外輸入限制 | | :------: | :----: | ------------ | | 1 | $11$ | 輸入滿足 $m, n \le 1000$。 | | 2 | $41$ | 輸入滿足 $m, n \le 10^5$。 | | 3 | $48$ | 無額外限制。 |