P11828 [TOIP2024] 距离函数
题目描述
小明和小花各有一棵 $n$ 个节点的有根树,其中小明的树满足节点 $i$ 的父节点为 $p_i$、根节点的 $p_i$ 为 $0$;小花的树满足节点 $i$ 的父节点为 $q_i$、根节点的 $q_i$ 为 $0$。他们想要知道彼此的有根树有多相似,为了明确定义相似程度,他们两人共同设计了一个两棵有根树的「距离函数」,只要距离函数给出的值越大,就表示这两棵树越不相似。
为了同时兼顾树的长相及编号的差异,距离函数大量考虑了「互为祖先关系」的节点对。详细地说,在一棵有根树 $T$ 上,当两个节点 $u, v$ 满足 $u$ 落在 $v$ 不断往父节点移动到根节点的路径上时,我们就称 $u$ 为 $v$ 在 $T$ 上的祖先;而当一对节点 $\{u, v\}$ 满足 $u$ 为 $v$ 在 $T$ 上的祖先、或 $v$ 为 $u$ 在 $T$ 上的祖先时,**$\{u, v\}$ 在 $T$ 即互为祖先关系**。
小明和小花将以上的距离函数应用在两棵树的情况下,只要一对节点 $\{u, v\}$ 满足他们在其中一棵树互为祖先关系、另一棵不是的话,他们就认为这两棵有根树的距离增加了。
不过这样的距离函数限制过于死板,为了容许误差的存在,两人又多加入了一个误差参数 $k$ 来进行函数值的调整,并牵涉到了计算「祖先关系距离」的子函数 $d_T(u, v)$,也就是说,我们可以计算两个节点 $\{u, v\}$ 在给定的有根树 $T$ 上距离「成为祖先关系」有多近。很显然的,当 $u, v$ 互为祖先关系时,他们的「祖先关系距离」即为 $0$;而当 $u, v$ 互不为祖先关系时,他们的祖先关系距离被定义成「最少的移动步数使得 $u, v$ 互为祖先关系」,白话地说,我们可以想象有两颗棋子分别摆在节点 $u$ 和 $v$ 上,每一步移动都可以把一颗棋子移动到所在节点的父节点上,而祖先关系距离即是最少的棋子移动次数使得两颗棋子能落在互为祖先关系的节点对上。
要计算 $u, v$ 在 $T$ 上的祖先关系距离 $d_T(u, v)$ 其实很单纯:先找出 $u, v$ 在 $T$ 上的「最近公共祖先」$\textrm{lca}(u, v)$,并取 $u$ 和 $v$ 分别往上移动到 $\textrm{lca}(u, v)$ 的步数中最小的那个即可。
有了祖先关系距离的定义,小明和小花的距离函数终于能够完整地定义清楚:
- 首先决定好一个误差参数 $k$,以及需要计算距离的两棵有根树 $S, T$。
- 当一对节点对 $\{u, v\}$ 满足他们在其中一棵树互为祖先关系、另一棵的祖先关系距离大于 $k$ 时,该节点对就被视为是有差异的节点对。
- 也就是说,「$d_S(u, v) = 0$ 且 $d_T(u, v)>k$」或「$d_T(u, v) = 0$ 且 $d_S(u, v) > k$」。
- 考虑所有 $\frac{N\times (N - 1)}{2}$ 组节点对,有差异的节点对数量即是 $S, T$ 的距离函数值。
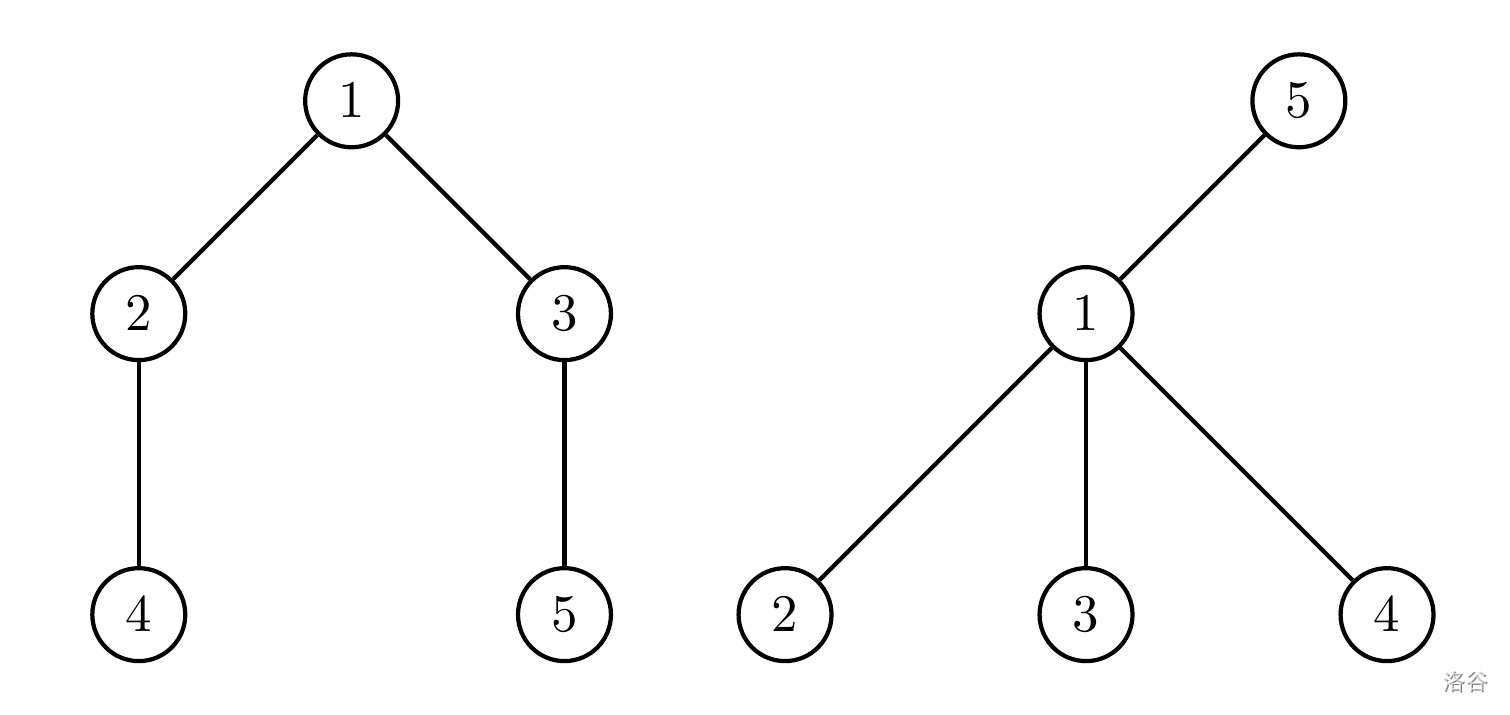
上图为范例测试数据一和二所给定的两棵有根树,左边的树以节点 $1$ 为根、右边的树以节点 $5$ 为根。以节点对 $\{2, 5\}$ 为例,我们可知在左树 $\textrm{lca}(2, 5)=1$,节点 $5$ 移动到节点 $1$ 需要两步,但节点 $2$ 移动到节点 $1$ 只需要一步,因此他们在左树的祖先关系距离为 $1$。注意到因为节点对 $\{2, 5\}$ 在右树互为祖先关系,当 $k=0$ 时,节点对 $\{2, 5\}$ 会被视为有差异的节点对,同理,节点对 $\{2, 4\}$ 以及 $\{4, 5\}$ 都是有差异的节点对,因此,上图中的两棵树在 $k=0$ 时的距离函数值为 $3$;而当 $k=1$ 时,只有 $\{4, 5\}$ 因在左树的祖先关系距离为 $2$ 会被视为有差异的节点对,距离函数值仅为 $1$。
请你编写一个程序,帮助小明和小花计算给定的两棵有根树在误差参数为 $k$ 时的距离函数值。
输入格式
> $n$ $k$
> $p_1$ $p_2$ $\cdots$ $p_n$
> $q_1$ $q_2$ $\cdots$ $q_n$
* $n$ 代表给定的树之大小。
* $k$ 代表这次量测两棵树距离时使用的误差参数。
* 在给定的第一棵树中,节点 $i$ 的父节点为 $p_i$。特别地,当 $p_i = 0$ 时,表示节点 $i$ 是第一棵树的根节点。
* 在给定的第二棵树中,节点 $i$ 的父节点为 $q_i$。特别地,当 $q_i = 0$ 时,表示节点 $i$ 是第二棵树的根节点。
输出格式
> $d$
* $d$ 为一整数,代表给定的两棵树在误差参数 $k$ 时的距离函数值。
说明/提示
### 测试数据限制
* $1 \le n \le 2\times 10^5$。
* $0 \le k < n$。
* $0 \le p_i, q_i \le n$。
* 保证存在唯一一个 $u$ 满足 $p_u = 0$,且序列 $p$ 形成一个以 $u$ 为根的有根树。
* 保证存在唯一一个 $v$ 满足 $q_v = 0$,且序列 $q$ 形成一个以 $v$ 为根的有根树。
* 输入的数均为整数。
### 评分说明
本题共有五组子任务,条件限制如下所示。
每一组可有一或多组测试数据,该组所有测试数据皆需答对才会获得该组分数。
| 子任务 | 分数 | 额外输入限制 |
| :------: | :----: | ------------ |
| 1 | $4$ | $n \le 100$。 |
| 2 | $10$ | $n \le 3000$。 |
| 3 | $32$ | $k = 0$。 |
| 4 | $25$ | $k \le 20$。 |
| 5 | $29$ | 无额外限制。 |