P11828 [TOIP2024] 距離函數

小明和小花各有一棵 $n$ 個節點的有根樹，其中小明的樹滿足節點 $i$ 的父節點為 $p_i$、根節點的 $p_i$ 為 $0$；小花的樹滿足節點 $i$ 的父節點為 $q_i$、根節點的 $q_i$ 為 $0$。他們想要知道彼此的有根樹有多相似，為了明確定義相似程度，他們兩人共同設計了一個兩棵有根樹的「距離函數」，只要距離函數給出的值越大，就表示這兩棵樹越不相似。 為了同時兼顧樹的長相及編號的差異，距離函數大量考慮了「互為祖先關係」的節點對。詳細地說，在一棵有根樹 $T$ 上，當兩個節點 $u, v$ 滿足 $u$ 落在 $v$ 不斷往父節點移動到根節點的路徑上時，我們就稱 $u$ 為 $v$ 在 $T$ 上的祖先；而當一對節點 $\{u, v\}$ 滿足 $u$ 為 $v$ 在 $T$ 上的祖先、或 $v$ 為 $u$ 在 $T$ 上的祖先時，**$\{u, v\}$ 在 $T$ 即互為祖先關係**。 小明和小花將以上的距離函數運用在兩棵樹的情況下，只要一對節點 $\{u, v\}$ 滿足他們在其中一棵樹互為祖先關係、另一棵不是的話，他們就認為這兩棵有根樹的距離增加了。 不過這樣的距離函數限制過於死板，為了容許誤差的存在，兩人又多加入了一個誤差參數 $k$ 來進行函數值的調整，並牽扯到了計算「祖先關係距離」的子函數 $d_T(u, v)$，也就是說，我們可以計算兩個節點 $\{u, v\}$ 在給定的有根樹 $T$ 上距離「成為祖先關係」有多近。很顯然的，當 $u, v$ 互為祖先關係時，他們的「祖先關係距離」即為 $0$；而當 $u, v$ 互不為祖先關係時，他們的祖先關係距離被定義成「最少的移動步數使得 $u, v$ 互為祖先關係」，白話地說，我們可以想像有兩顆棋子分別擺在節點 $u$ 和 $v$ 上，每一步移動都可以把一顆棋子移動到所在節點的父節點上，而祖先關係距離即是最少的棋子移動次數使得兩顆棋子能落在互為祖先關係的節點對上。 要計算 $u, v$ 在 $T$ 上的祖先關係距離 $d_T(u, v)$ 其實很單純：先找出 $u, v$ 在 $T$ 上的「最低共同祖先」$\textrm{lca}(u, v)$，並取 $u$ 和 $v$ 分別往上移動到 $\textrm{lca}(u, v)$ 的步數中最小的那個即可。 有了祖先關係距離的定義，小明和小花的距離函數終於能夠完整的定義清楚： - 首先決定好一個誤差參數 $k$，以及需要計算距離的兩棵有根樹 $S, T$。 - 當一對節點對 $\{u, v\}$ 滿足他們在其中一棵樹互為祖先關係、另一棵的祖先關係距離大於 $k$ 時，該節點對就被視為是有差異的節點對。 - 也就是說，「$d_S(u, v) = 0$ 且 $d_T(u, v)>k$」或「$d_T(u, v) = 0$ 且 $d_S(u, v) > k$」。 - 考慮所有 $\frac{N\times (N - 1)}{2}$ 組節點對，有差異的節點對數量即是 $S, T$ 的距離函數值。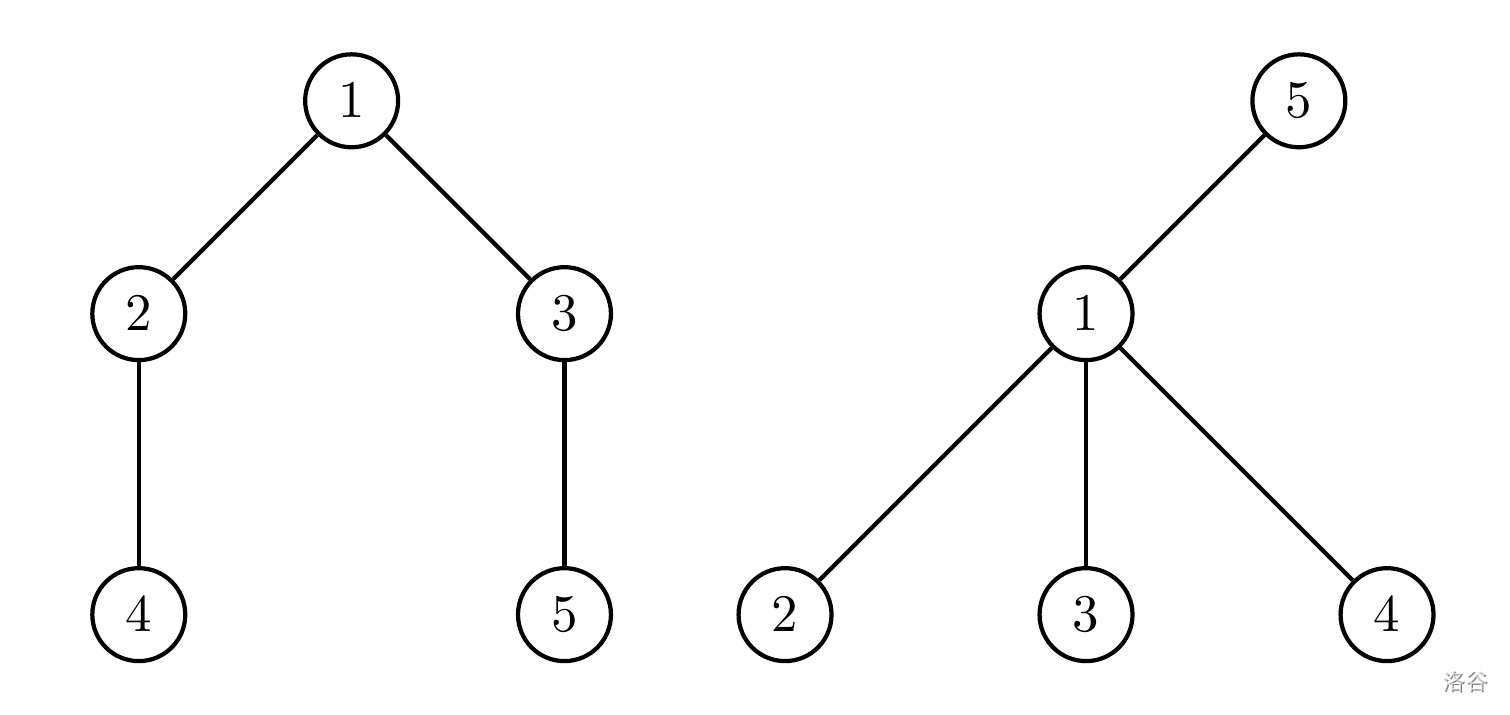  上圖為範例測試資料一和二所給定的兩棵有根樹，左邊的樹以節點 $1$ 為根、右邊的樹以節點 $5$ 為根。以節點對 $\{2, 5\}$ 為例，我們可知在左樹 $\textrm{lca}(2, 5)=1$，節點 $5$ 移動到節點 $1$ 需要兩步，但節點 $2$ 移動到節點 $1$ 只需要一步，因此他們在左樹的祖先關係距離為 $1$。注意到因為節點對 $\{2, 5\}$ 在右樹互為祖先關係，當 $k=0$ 時，節點對 $\{2, 5\}$ 會被視為有差異的節點對，同理，節點對 $\{2, 4\}$ 以及 $\{4, 5\}$ 都是有差異的節點對，因此，上圖中的兩棵樹在 $k=0$ 時的距離函數值為 $3$；而當 $k=1$ 時，只有 $\{4, 5\}$ 因在左樹的祖先關係距離為 $2$ 會被視為有差異的節點對，距離函數值僅為 $1$。 請你撰寫一支程式，幫助小明和小花計算給定的兩棵有根樹在誤差參數為 $k$ 時的距離函數值。

> $n$ $k$ > $p_1$ $p_2$ $\cdots$ $p_n$ > $q_1$ $q_2$ $\cdots$ $q_n$ * $n$ 代表給定的樹之大小。 * $k$ 代表這次量測兩棵樹距離時使用的誤差參數。 * 在給定的第一棵樹中，節點 $i$ 的父節點為 $p_i$。特別地，當 $p_i = 0$ 時，表示節點 $i$ 是第一棵樹的根節點。 * 在給定的第二棵樹中，節點 $i$ 的父節點為 $q_i$。特別地，當 $q_i = 0$ 時，表示節點 $i$ 是第二棵樹的根節點。

> $d$ * $d$ 為一整數，代表給定的兩棵樹在誤差參數 $k$ 時的距離函數值。

### 測資限制 * $1 \le n \le 2\times 10^5$。 * $0 \le k < n$。 * $0 \le p_i, q_i \le n$。 * 保證存在唯一一個 $u$ 滿足 $p_u = 0$，且序列 $p$ 形成一個以 $u$ 為根的有根樹。 * 保證存在唯一一個 $v$ 滿足 $q_v = 0$，且序列 $q$ 形成一個以 $v$ 為根的有根樹。 * 輸入的數皆為整數。 ### 評分說明 本題共有五組子任務，條件限制如下所示。 每一組可有一或多筆測試資料，該組所有測試資料皆需答對才會獲得該組分數。 | 子任務 | 分數 | 額外輸入限制 | | :------: | :----: | ------------ | | 1 | $4$ | $n \le 100$。 | | 2 | $10$ | $n \le 3000$。 | | 3 | $32$ | $k = 0$。 | | 4 | $25$ | $k \le 20$。 | | 5 | $29$ | 無額外限制。 |