P11829 [TOIP2024] 棲息地分配

有 $n$ 隻貓活動於某個地區，每隻貓各有其棲息地，編號為 $1$ 到 $n$。棲息地之間有 $m$ 條道路連接，道路總數不超過 $2n-4$。第 $i$ 條道路連接第 $a_i$ 個棲息地和第 $b_i$ 個棲息地，貓可以沿著這些道路在棲息地之間**雙向**移動，且不會有兩條不同的道路連接著同一對棲息地。有 $3$ 個動保團體要接管此地區，請你協助將這 $n$ 個棲息地分配給這 $3$ 個團體，滿足以下要求： - 每個棲息地僅由 $1$ 個團體管理，且每個團體需要管理至少 $1$ 個棲息地。每個團體所屬的棲息地之間不一定要連通。 - 為了方便管理，每個團體會移除由該團體負責的棲息地之間的道路。換句話說，若有一條道路連接的兩個棲息地被分配到同一個團體，該道路會被移除。 - 這些道路移除後，剩餘的道路不可以形成「環」，以免貓可能會繞著環奔跑，讓工作人員難以捉捕。也就是說，不可以存在一個兩兩相異的棲息地序列 $v_1,v_2,\ldots, v_k$，滿足 $k \ge 3$，且對於所有 $1\le i < k$，棲息地 $v_i$ 和棲息地 $v_{i+1}$ 都有一條未被移除的道路連接、同時 $v_k$ 和 $v_1$ 也有一條未被移除的道路連接。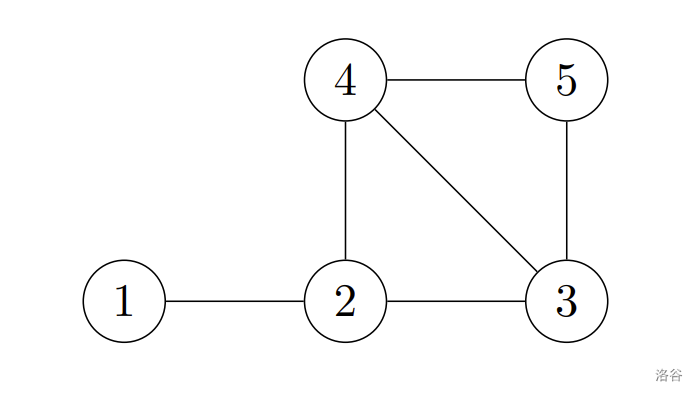 舉例，有 $5$ 個棲息地，道路連接如下圖所示  我們可以將第 $3$, $4$, $5$ 個棲息地分配給第 $1$ 個團體，第 $1$ 個棲息地分配給第 $2$ 個團體，第 $2$ 個棲息地分配給第 $3$ 個團體。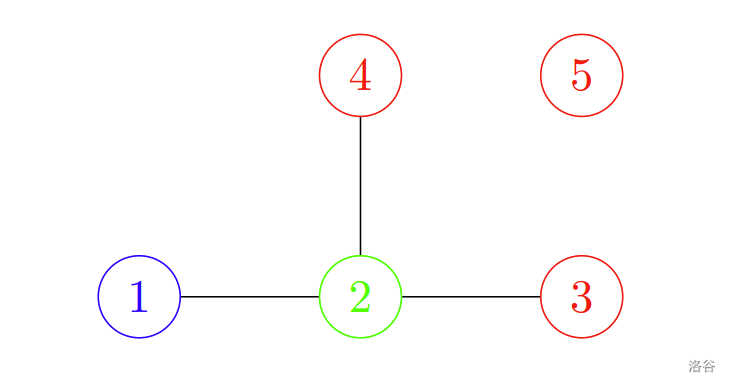 移除掉道路後，如下圖所示  剩餘道路不存在環，所以這是一種滿足目標的分配方式。 請輸出這 $3$ 個團體應該分別管理哪些棲息地，若有多種分配方式滿足條件，輸出任意一種。

> $t$ > $test_1$ > $test_2$ > $\vdots$ > $test_t$ * $t$ 表示測試資料個數。 * $test_i$ 為第 $i$ 筆測試資料。 每一筆測試資料的輸入格式如下： > $n$ $m$ > $a_1$ $b_1$ > $a_2$ $b_2$ > $\vdots$ > $a_m$ $b_m$ * $n$ 為貓的棲息地數量。 * $m$ 為道路數量。 * $a_i, b_i$ 為第 $i$ 條道路連接的棲息地編號。不會有兩條不同的道路連接著同一對棲息地。

輸出 $t$ 筆測試資料之答案： > $answer_1$ > $answer_2$ > $\vdots$ > $answer_t$ * $answer_i$ 為第 $i$ 筆測試資料之答案。 每一筆測試資料答案的輸出格式如下 > $k_1$ $c_{1,1}$ $\cdots$ $c_{1,k_1}$ > $k_2$ $c_{2,1}$ $\cdots$ $c_{1,k_2}$ > $k_3$ $c_{3,1}$ $\cdots$ $c_{1,k_3}$ * $k_i$ 為第 $i$ 個團體分配到的棲息地總數。 * $c_{i,j}$ 為第 $i$ 個團體分配到的第 $j$ 個棲息地。 若該筆測試資料不存在所求的分法，請輸出 -1。

### 測資限制 * $1 \le t \le 3\times 10^5$。 * $3 \le n \le 3\times 10^5$。 * $0 \le m \le 2n - 4$。 * $1 \le a_i, b_i \le n$，$a_i \neq b_i$。 * 所有測試資料中，$n$ 的總和不超過 $3\times 10^5$。 ### 評分說明 本題共有四組子任務，條件限制如下所示。 每一組可有一或多筆測試資料，該組所有測試資料皆需答對才會獲得該組分數。 | 子任務 | 分數 | 額外輸入限制 | | :------: | :----: | ------------ | | 1 | $3$ | 輸入滿足 $m = n - 1$，且所有的棲息地連通。 | | 2 | $23$ | 輸入保證存在兩個以上的棲息地互相無法抵達。 | | 3 | $28$ | 輸入滿足所有測試資料中，$n$ 的總和不超過 $500$。 | | 4 | $46$ | 無額外限制。 |