P11848 [TOIP 2023] 房屋推荐

房屋中介小潮负责高谈市的租房业务。小潮手中有编号为 $1, 2, \cdots, n$ 的 $n$ 间待租房屋，房屋 $i$ 的位置用二维坐标 $(a_i, b_i)$ 表示，且该房屋的月租金为 $r_i$ 元。 高谈市有 $m$ 座地铁站，地铁站编号为 $1, 2, \cdots, m$，地铁站 $j$ 的位置用二维坐标 $(c_j, d_j)$ 表示。定义房屋 $i$ 与地铁站 $j$ 的距离为 $\sqrt{(a_i - c_j)^2 + (b_i - d_j)^2}$ 单位。 小潮发现租客的偏好如下： 1. 房屋与最近地铁站的距离越短越好。 2. 若两间房屋离各自最近地铁站的距离相同，则月租金较低的房屋更优。 3. 若两间房屋离各自最近地铁站的距离相同且月租金相同，则编号较小的房屋更优。 请帮助小潮开发一个房屋推荐系统，对房屋进行排序，使得越受租客偏好的房屋排名越靠前。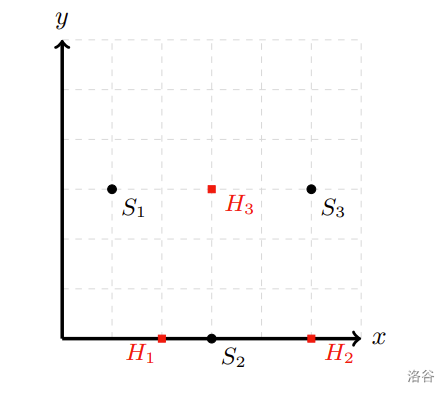 下图为一个 $n=3$ 且 $m=3$ 的示例： - 方点 $H_1, H_2, H_3$ 分别代表房屋 $1, 2, 3$ - 圆点 $S_1, S_2, S_3$ 分别代表地铁站 $1, 2, 3$ - 房屋坐标与租金： - 房屋 1：$(2, 0)$，租金 $11000$ 元 - 房屋 2：$(5, 0)$，租金 $12000$ 元 - 房屋 3：$(3, 3)$，租金 $10000$ 元 - 地铁站坐标： - 地铁站 1：$(1, 3)$ - 地铁站 2：$(3, 0)$ - 地铁站 3：$(5, 3)$  计算得出： - 房屋 $1$ 最近地铁站为 $2$ 号站（距离 $1$ 单位） - 房屋 $2$ 最近地铁站为 $2$ 号站（距离 $2$ 单位） - 房屋 $3$ 最近地铁站为 $1$ 号站和 $3$ 号站（距离 $2$ 单位） 第 $2$ 间房屋和第 $3$ 间房屋与地铁站的距离均为 $2$ 单位，但由于第 $3$ 间房屋的月租金更便宜，因此排在第 $2$ 间房屋前面。最终租客偏好的房屋顺序为：$1, 3, 2$。

> $n$ $m$ > $a_1$ $b_1$ $r_1$ > $a_2$ $b_2$ $r_2$ > $\vdots$ > $a_n$ $b_n$ $r_n$ > $c_1$ $d_1$ > $c_2$ $d_2$ > $\vdots$ > $c_m$ $d_m$ * $n, m$ 分别表示房屋与地铁站的数量 * 房屋 $i$ 的坐标为 $(a_i, b_i)$，租金为 $r_i$ * 地铁站 $j$ 的坐标为 $(c_j, d_j)$

> $p_1$ > $p_2$ > $\vdots$ > $p_n$ * 输出按排名顺序的房屋编号

### 测试数据限制 - $1 \le n \le 10^5$ - $1 \le m \le 10^3$ - $-10^9 \le a_i, b_i, c_i, d_i \le 10^9$ - $0 \le r_i \le 10^9$ - 所有坐标为整数且互不重叠 - 保证房屋与地铁站不在同一坐标 ### 评分规则 | 子任务 | 分数 | 条件 | | :----: | :--: | ------------- | | 1 | 20 | $n \le 2$ | | 2 | 30 | $n \le 100$ | | 3 | 50 | 无额外限制 |