P11850 [TOIP 2023] 关卡地图

许多游戏的设计是以关卡为单位，玩家通过一个关卡后才能挑战下一个关卡。这些关卡的解锁关系有时并不是线性的，也就是玩家通过一个关卡后可能一次开放多个可以挑战的新关卡，也可能不会开放任何新关卡。 经典的 A 游戏就属于这种非线性的关卡结构。关卡的状态分为三种：「尚未解锁」、「已解锁但未通过」以及「已通过」。A 游戏有 $n$ 个关卡，被呈现在一张地图上，其中有 $m$ 对关卡存在相互解锁关系，以 $(u_i, v_i)$ 表示。当玩家通过关卡 $u_i$ 时，关卡 $v_i$ 将被解锁；反过来，当玩家通过关卡 $v_i$ 时，关卡 $u_i$ 也会被解锁。玩家可以从任意关卡开始游戏，且保证在非线性的玩法下，可以通过其他所有关卡。另外，为了避免通关流程过于简单，A 游戏满足 $m \le n$。 凯特决定把 A 游戏当作线性解锁关卡来玩：选择一个起始关卡，接着一旦通过了某个关卡 $c$ 后，下一关**只能是与关卡 $c$ 有相互解锁关系的关卡**，且**一关最多只能通过一次**。已知凯特通过关卡 $i$ 时，得到的成就感为 $a_i$，请帮他找出最适合的通关路径以最大化成就感总和。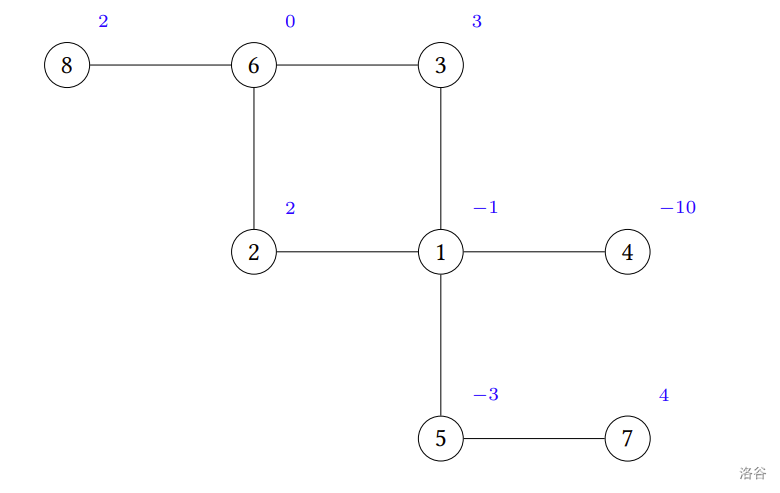 举例来说，假设 A 游戏的关卡地图如下图所示，图中圆点中的数字代表关卡编号，圆点旁边的数字代表该关卡通关所得到的成就感；两个关卡的连线代表一个相互解锁关系。若凯特选择从关卡 $7$ 开始通关，则关卡 $5$ 将被解锁，接着依序通过关卡 $5, 1, 3, 6, 2$，得到的成就感总和为 $4+(-3)+(-1)+3+0+2 = 5$。另一方面，若凯特选择从关卡 $8$ 开始通关，并依序通过关卡 $6, 3, 1, 2$，得到的成就感总和为 $2+0+3+(-1)+2 = 6$，此时成就感总和为最大值。 

> $n$ $m$ > $u_1$ $v_1$ > $u_2$ $v_2$ > $\vdots$ > $u_m$ $v_m$ > $a_1$ $a_2$ $\ldots$ $a_n$ * $n$ 代表关卡数。 * $m$ 代表解锁关系数。 * $u_i, v_i$ 代表通过关卡 $u_i$ 或 $v_i$ 的其中一个后，另一个关卡将被解锁。 * $a_i$ 代表凯特通过关卡 $i$ 时的成就感。

> $s$ * $s$ 为一整数，代表凯特能获得的最大成就感总和。

### 测试数据限制 * $1 \le n \le 10^5$。 * $m = n-1$ 或 $m = n$。 * $1 \le u_i < v_i \le n$，且若 $i \ne j$，保证 $(u_i, v_i) \ne (u_j, v_j)$。 * $-10^9 \le a_i \le 10^9$。 * 游戏设计保证正常游玩（非线性）时从任何一关作为起始关卡皆能解锁所有关卡。 * 上述变量均为整数。 ### 评分说明 本题共有四组子任务，条件限制如下所示。 每一组可有一或多组测试数据，该组所有测试数据皆需答对才会获得该组分数。 | 子任务 | 分数 | 额外输入限制 | | :------: | :----: | ------------ | | 1 | $17$ | $n \le 100$ | | 2 | $23$ | $m = n-1$ | | 3 | $34$ | $a_i \ge 0$ | | 4 | $26$ | 无额外限制 |