P11850 [TOIP 2023] 關卡地圖

許多遊戲的設計是以關卡為單位，玩家通過一個關卡後才能挑戰下一個關卡。這些關卡的解鎖關係有時並不是線性的，也就是玩家通過一個關卡後可能一次開放多個可以挑戰的新關卡，也可能不會開放任何新關卡。 經典的 A 遊戲就屬於這種非線性的關卡結構。關卡的狀態分為三種：「尚未解鎖」、「已解鎖但未通過」以及「已通過」。A 遊戲有 $n$ 個關卡，被呈現在一張地圖上，其中有 $m$ 對關卡存在相互解鎖關係，以 $(u_i, v_i)$ 表示。當玩家通過關卡 $u_i$ 時，關卡 $v_i$ 將被解鎖；反過來說，當玩家通過關卡 $v_i$ 時，關卡 $u_i$ 也會被解鎖。玩家可以從任意關卡開始遊戲，且保證在非線性的玩法下，可以通過其他所有關卡。另，為了避免破關流程過於簡單，A 遊戲滿足 $m \le n$。 凱特決定把 A 遊戲當作線性解鎖關卡來玩：選擇一個起始關卡，接著一旦通過了某個關卡 $c$ 後，下一關**只能是與關卡 $c$ 有相互解鎖關係的關卡**，且**一關最多只能通過一次**。已知凱特通過關卡 $i$ 時，得到的成就感為 $a_i$，請幫他找出最適合的破關路徑以最大化成就感總和。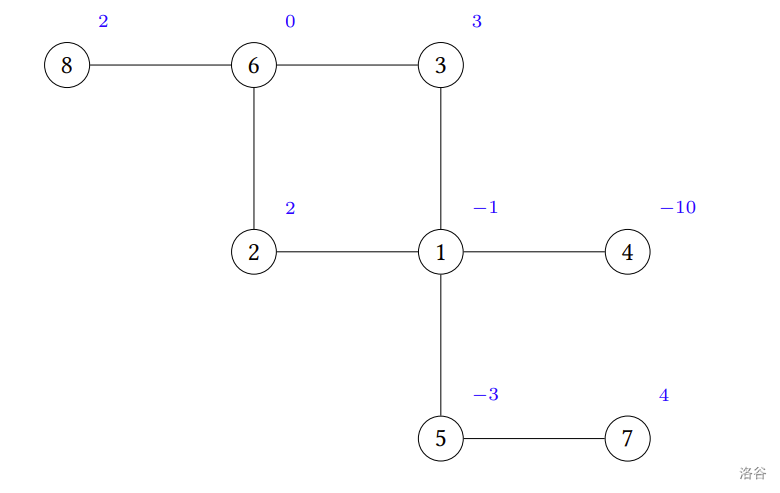 舉例來說，假設 A 遊戲的關卡地圖如下圖所示，圖中圓點中的數字代表關卡編號，圓點旁邊的數字代表該關卡破關所得到的成就感；兩個關卡的連線代表一個相互解鎖關係。若凱特選擇從關卡 $7$ 開始破關，則關卡 $5$ 將被解鎖，接著依序通過關卡 $5, 1, 3, 6, 2$，得到的成就感總和為 $4+(-3)+(-1)+3+0+2 = 5$。另一方面，若凱特選擇從關卡 $8$ 開始破關，並依序通過關卡 $6, 3, 1, 2$，得到的成就感總合為 $2+0+3+(-1)+2 = 6$，此時成就感總和為最大值。 

> $n$ $m$ > $u_1$ $v_1$ > $u_2$ $v_2$ > $\vdots$ > $u_m$ $v_m$ > $a_1$ $a_2$ $\ldots$ $a_n$ * $n$ 代表關卡數。 * $m$ 代表解鎖關係數。 * $u_i, v_i$ 代表通過關卡 $u_i$ 或 $v_i$ 的其中一個後，另一個關卡將被解鎖。 * $a_i$ 代表凱特通過關卡 $i$ 時的成就感。

> $s$ * $s$ 為一整數，代表凱特能獲得的最大成就感總和。

* $1 \le n \le 10^5$。 * $m = n-1$ 或 $m = n$。 * $1 \le u_i < v_i \le n$，且若 $i \ne j$，保證 $(u_i, v_i) \ne (u_j, v_j)$。 * $-10^9 \le a_i \le 10^9$。 * 遊戲設計保證正常遊玩（非線性）時從任何一關做為起始關卡皆能解鎖所有關卡。 * 上述變數都是整數。 ### 評分說明 本題共有四組子任務，條件限制如下所示。 每一組可有一或多筆測試資料，該組所有測試資料皆需答對才會獲得該組分數。 | 子任務 | 分數 | 額外輸入限制 | | :------: | :----: | ------------ | | 1 | $17$ | $n \le 100$ | | 2 | $23$ | $m = n-1$ | | 3 | $34$ | $a_i \ge 0$ | | 4 | $26$ | 無額外限制 |