P11852 [TOIP 2023] 公路

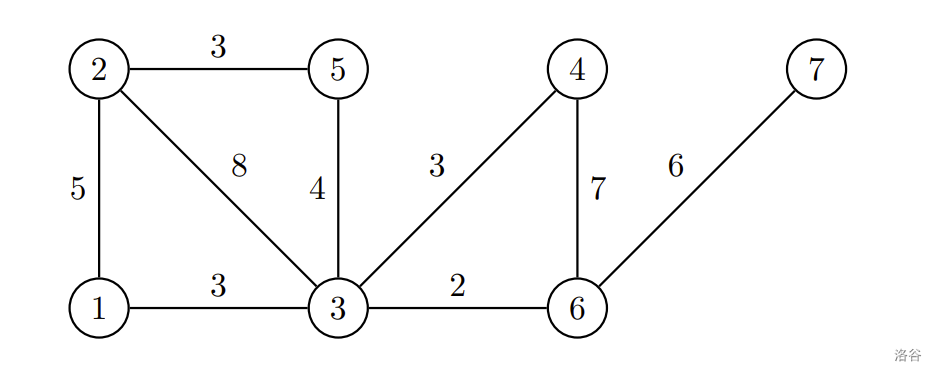
某国的公路网由 $n$ 个城镇（编号 $1\sim n$）和 $m$ 条连接两个相异城镇的双向公路组成，每条公路有其长度，以公里表示。最近该国流行起电动车，但是公路之间都没有充电站，电动车只能在城镇充电。该国交通部门官员十分担心有些被观光局规划好的旅程会使电动车的续航力没办法走完一条公路，也因此，官员希望旅程中使用到的最长公路长度要尽量短，否则若有些电动车的实际续航力低于一段公路的长度，它们一定会在公路中间没电。 对于一趟被规划好的旅程，观光局会为其决定好一个起点 $u$ 和终点 $v$，并找出 $\textbf{两条}$ 由 $u$ 到 $v$ $\textbf{公路相互不重复}$ 的路径，来作为一个完整的旅程规划。例如下图是一个 $n=7$、$m=9$ 的例子，点上标示城镇的编号，边上标示公路的长度。  若要规划城镇 $1$ 到城镇 $2$ 的旅程，可以采用以下两条路径： - $1\to 2$ 以及 $1\to 3\to 2$ 这两条路径中，所使用到的最长公路长度是 $8$ 公里，但若采用以下两条路径： - $1\to 2$ 以及 $1\to 3\to 5\to 2$ 就可以将使用的最长公路长度降低至 $5$，也是使最长公路最短的选择方式。而若要规划城镇 $1$ 到城镇 $6$ 的旅程，可以采用以下两条路径： - $1\to 3\to 6$ 以及 $1\to 2\to 5\to 3\to 4\to 6$ 使用的最长公路长度是 $7$，同时也是使最长公路最短的选择方式，注意到虽然这两条路径共用了同一个城镇 $3$，但条件只要求“使用的公路不重复”，因此为一种满足条件的路径选择方式。 一个旅程的两条路径所使用的最长公路愈短，则该旅程愈佳。今给定 $q$ 对起终点，请写程序计算每对起终点之最佳旅程使用到的最长公路长度，或者回报不存在任何一种路径的选择方式。

> $n$ $m$ > $a_1$ $b_1$ $l_1$ > $a_2$ $b_2$ $l_2$ > $\vdots$ > $a_m$ $b_m$ $l_m$ > $q$ > $u_1$ $v_1$ > $u_2$ $v_2$ > $\vdots$ > $u_q$ $v_q$ * $n$, $m$ 分别代表城镇和公路的数量。 * 第 $i$ 条公路连接着城镇 $a_i$ 和 $b_i$，且长度为 $l_i$ 公里。 * $q$ 代表预计规划的旅程数量。 * 第 $i$ 个旅程预计选择 $u_i$ 作为起点、$v_i$ 作为终点。

> $p_1$ > $p_2$ > $\vdots$ > $p_q$ * $p_i$ 为一整数 * 若 $p_i = -1$，则表示不存在路径的选择方法可以完整的规划第 $i$ 个旅程。 * 否则，$p_i$ 代表在最佳的路径选择方式下，第 $i$ 个旅程所使用到的最长公路长度最小值。

### 数据限制 * $2 \le n \le 1000$。 * $n - 1 \le m \le \displaystyle\frac{n\times (n-1)}{2}$。 * $1 \le a_i, b_i \le n$，$a_i \ne b_i$。 * $1 \le l_i \le 10^9$。 * 不会有两条公路连接着相同的一组城镇。 * $1 \le q \le 5\times 10^5$。 * $1 \le u_i, v_i \le n$，$u_i \ne v_i$。 * 输入的数皆为整数。 * 保证任两个城镇可以通过若干条公路直接或间接抵达。 ### 评分说明 本题共有四组子任务，条件限制如下所示。每一组可有一或多个测试数据，该组所有测试数据皆需答对才会获得该组分数。 | 子任务 | 分数 | 额外输入限制 | | :------: | :----: | ------------ | | 1 | $18$ | $n \le 100$，$m, q \le 300$，$l_i = 1$ | | 2 | $31$ | $n \le 500$，$m, q \le 1000$ | | 3 | $22$ | $m\le 3000$ | | 4 | $29$ | 无额外限制 |