P11892 [XRCOI Round 1] C. 草萤有耀终非火

> 草萤有耀终非火，荷露虽团岂是珠？

小 G 和小 Z 在一个 $n$ 行 $m$ 列的网格图上摆满了熄灭的灯，并在其中 $k$ 盏灯中放置了燃料。但是它们均没有被点燃。我们用 $(i,j)$ 表示**从下往上**第 $i$ 行**从左往右**第 $j$ 列的格子。 这些灯在点亮时会出现某些奇怪的现象：假设 $a,b,x,y$ 均为正整数，当 $(x,y),(x+a,y),(x,y+b),(x+a,y+b)$ 四个格子中有三个格子中的灯都**已点亮**且 $1 \le x < x+a \le n,1 \le y < y+b \le m$，那么剩下的那一个格子的灯就会自动被点亮。 因此，一盏灯既可以在一开始时通过点燃燃料的方式点亮，又可以通过这种现象点亮。 现在他们想要把放有火炬台的格子 $(1,1)$ 和 $(1,m)$ 中的灯点亮。而你需要求出把格子 $(1,1)$ 和 $(1,m)$ 中的灯都点亮时，**一开始**最少要点燃几盏灯中的燃料（不含过程中通过这种现象点亮的），或者报告无法把格子 $(1,1)$ 或 $(1,m)$ 中的灯点亮。 注意：同一盏灯中可能放置多个燃料，但只要点燃一个燃料这盏灯就可以被点亮。

无

无

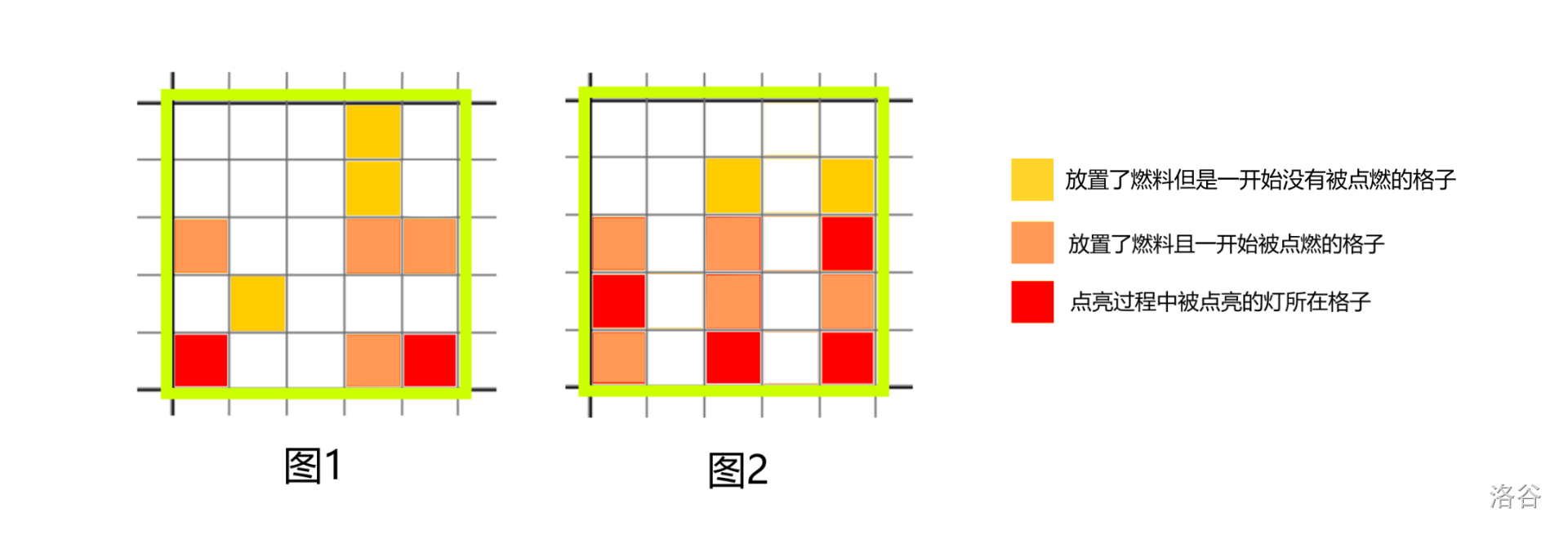
#### 样例解释  对于第一组样例：可以选择格子 $(3,1),(3,4),(1,4),(3,5)$ 中的燃料点燃，如图 $1$ 所示。 对于第二组样例：可以选择格子 $(1,1),(3,1),(3,3),(2,3),(2,5)$ 中的燃料点燃，如图 $2$ 所示。 对于第三组样例：可以选择格子 $(1,1),(1,5)$ 中的燃料点燃。 对于第四组样例：显然没有合法的方案。 对于第五组样例：此时格子 $(1,1)$ 与 $(1,m)$ 是同一个格子，因此只要选择格子 $(1,1)$ 中的一个燃料点燃即可。并且注意数据中可能出现同一盏灯中有多个燃料的情况。 #### 数据规模与约定 **本题采用捆绑测试。** 其中子任务 $0$ 为样例，记 $0$ 分。 | Subtask 编号 | $t\le $ | $n,m \le $ | $\sum n,\sum m \le$ | $k \le $ | $\sum k \le$ | 特殊性质 | 得分 | | :-------: | :-----------: | :--------: | :--------: | :--------: | :--------: | :--------: | :-----: | | $1$ | $10$ | $10$ | $100$ | $10$ | $100$ | 无 | $20$ | | $2$ | $10$ | $10^3$ | $10^4$ | $5\times 10^3$ | $2\times10^4$ | $A$ | $2$ | | $3$ | $5\times 10^3$ | $10^5$ | $10^6$ | $5\times10^5$ | $2\times10^6$ | $B$ | $2$ | | $4$ | $5\times 10^3$ | $10^5$ | $10^6$ | $5\times 10^5$ | $2\times10^6$ | $C$ | $15$ | | $5$ | $10^3$ | $10^3$ | $10^4$ | $5\times 10^3$ | $2\times 10^4$ | 无 | $26$ | | $6$ | $5\times 10^3$ | $10^5$ | $10^6$ | $5\times 10^5$ | $2\times 10^6$ | 无 | $35$ | 特殊性质 $A$：保证格子 $(1,1),(1,m)$ 放有燃料。 特殊性质 $B$：保证放置的燃料中没有两个燃料是同一行或者同一列的。 特殊性质 $C$：保证一定存在某一列摆满了燃料。 对于 $100\%$ 的数据：保证 $1 \le t \le 5\times10^3,1 \le n,m \le 10^5,0 \le k \le 2\times10^6,1 \le \sum n,\sum m \le 10^6,0 \le \sum k \le 2\times 10^6,1\le x \le n,1 \le y \le m$。