P11902 [NHSPC 2023] A. 演化树分析
题目描述
彼得是一位生物学家。有次他在两笔资料中分析同一群现存物种集合 $\Sigma = \{1, 2, \ldots, n\}$ 间的演化关系,却得到了不太一样的演化树,想知道这两棵树的相似程度。
一棵演化树 $T$ 是一棵无向无根树 (undirected, unrooted tree),其中叶节点为现存物种 $1, 2, \ldots, n$,其他节点则为已灭绝物种。设 $v \in V(T)$,我们用 $\deg(v)$ 来表示与节点 $v$ 相邻的节点个数。在一棵演化树中,每个代表已灭绝物种的节点 $v$ 均有 $\deg(v) \ge 3$。对于一个现存物种的子集合 $X \subseteq \Sigma$,我们用 $T\{X\}$ 来代表 $X$ 中的现存物种在 $T$ 上的演化关系所形成的「演化子树」,构建方式如下:
1. 对所有 $X$ 中的任两点,标记其在 $T$ 上的简单路径,并将所有不在 $X$ 且未被标记的点删除以得到 $T'$。
1. 从 $T'$ 中不断删除满足 $\deg(v) = 2$ 的非叶节点 $v$ 以得到 $T\{X\}$:将与 $v$ 连接的两条边合并成一条,并移除 $v$。
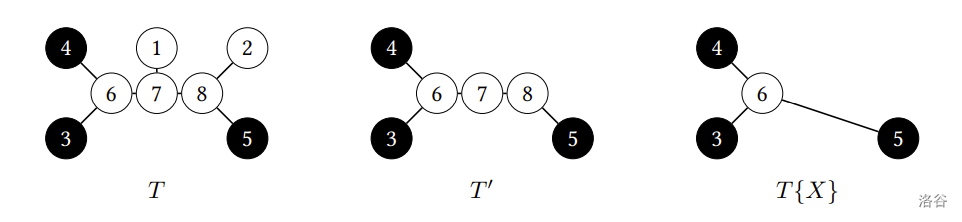
以下图的演化树 $T$ 为例。$T$ 里的现存物种集合为 $\Sigma = \{1, 2, 3, 4, 5\}$,若取 $X = \{3, 4, 5\}$,则经步骤 $1$ 后会得到 $T'$,再经过步骤 $2$ 后会得到 $T\{X\}$。注意当 $X = \emptyset$ 时,根据定义我们有 $T\{X\} = \emptyset$。
从一棵演化树 $T$ 中移除大小为 $k \ge 0$ 的任意边集合 $K$,可以得到 $k+1$ 棵子树 $T^{(1)}, T^{(2)}, \ldots, T^{(k+1)}$,其中每棵子树 $T^{(i)}$ 上的物种在 $T$ 中的演化关系都会构成一棵**演化子树**,我们称它们为从 $T$ 中移除 $K$ 所导出的**演化森林**。注意我们有
1. $T$ 自身为移除 $\emptyset$ 后导出的演化森林。
1. 若一棵子树 $T^{(i)}$ 上没有任何现存物种,对应的演化子树为空。
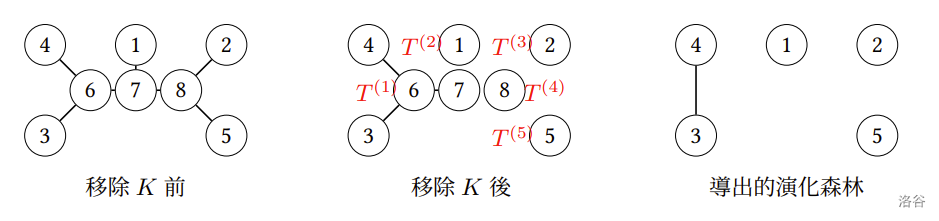
以上图中的 $T$ 为例,移除 $K = \{(1, 7), (7, 8), (2, 8), (5, 8)\}$ 四条边可以得到五棵子树 $T^{(1)}, T^{(2)}, \ldots, T^{(5)}$,接着导出演化森林:
比较两座现存物种相同的演化森林时,我们只关注现存物种间的联系,因此已灭绝物种(即非叶节点)的编号并不重要。设 $F_1$ 与 $F_2$ 为两座现存物种相同的演化森林,若移除它们的非叶节点编号后变得完全相同,我们就称 $F_1$ 与 $F_2$ 相似。更精确地说,我们称 $F_1$ 与 $F_2$ 相似,若且唯若存在某个一一映射 $\Phi: V(F_1) \to V(F_2)$,满足
1. 对任意 $u \in \Sigma = \{1, 2, \ldots, n\}$,我们有 $\Phi(u) = u$。
1. 对任意 $u, v \in V(F_1)$,我们有
$$(u, v) \in E(F_1) \iff (\Phi(u), \Phi(v)) \in E(F_2).$$
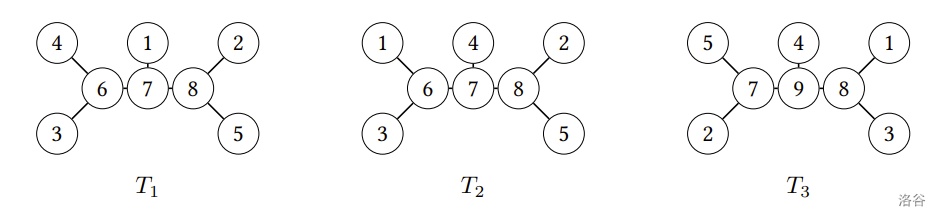
以下图为例,如果将 $T_1, T_2, T_3$ 的非叶节点编号都移除,会发现 $T_1$ 与 $T_2$ 不相似,而 $T_2$ 与 $T_3$ 相似。
设 $T_1$ 与 $T_2$ 为现存物种相同的两棵演化树。若存在从 $T_1$ 与 $T_2$ 中各删除 $k$ 条边的方法,使得两者导出的演化森林相似,则称 $T_1$ 与 $T_2$ 的差异不大于 $k$,而满足此条件的最小整数 $k^*$ 称为 $T_1$ 与 $T_2$ 的**差异数**。如上图中 $T_2$ 与 $T_3$ 的差异数为 $0$,而 $T_1$ 与 $T_2$ 的差异数为 $1$。
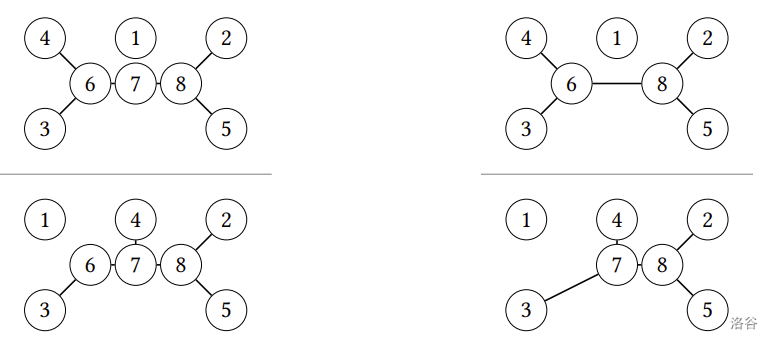
从 $T_1$ 与 $T_2$ 各删除 $1$ 条边 | 导出了相似的演化森林
设从 $T_1$ 与 $T_2$ 中删除的边集合分别为 $K_1$ 与 $K_2$,两种删除方法被视作不同若且唯若 $K_1$ 不同或 $K_2$ 不同。现给定两棵物种集合均为 $\Sigma$ 的演化树 $T_1, T_2$ 以及一个整数上限 $k$,彼得想知道它们的差异数 $k^*$ 是否不大于 $k$;如果 $1 \le k^* \le k$,彼得也想知道有多少种从 $T_1$ 和 $T_2$ 中各删除 $k^*$ 条边的方法,可以使它们导出相似的演化森林。
输入格式
> $n$ $m_1$ $m_2$ $k$
> $u_1$ $v_1$
> $u_2$ $v_2$
> $\vdots$
> $u_{n+m_1-1}$ $v_{n+m_1-1}$
> $u_1'$ $v_1'$
> $u_2'$ $v_2'$
> $\vdots$
> $u_{n+m_2-1}'$ $v_{n+m_2-1}'$
* $n$ 代表现存物种集合 $\Sigma = \{1, 2, \ldots, n\}$ 的大小。
* $m_1$ 代表在 $T_1$ 中已灭绝物种(以 $n+1, n+2, \ldots, n+m_1$ 表示)的数量。
* $m_2$ 代表在 $T_2$ 中已灭绝物种(以 $n+1, n+2, \ldots, n+m_2$ 表示)的数量。
* $k$ 代表彼得设定的上限。
* $u_i, v_i$ 代表 $T_1$ 有一条边从 $u_i$ 连接到 $v_i$。
* $u_i', v_i'$ 代表 $T_2$ 有一条边从 $u_i'$ 连接到 $v_i'$。
输出格式
如果 $k^* = 0$,请输出
> $0$
如果 $1 \le k^* \le k$,请输出
> $k^*$
> $S$
其中 $S$ 为一整数,代表从 $T_1$ 与 $T_2$ 中各删除 $k^*$ 条边后导出的演化森林相似的删除方法数。如果 $k^* > k$,请输出
> $-1$
说明/提示
### 测试数据限制
* $n \ge 2$。
* $0 \le m_1 \le 300-n$。
* $0 \le m_2 \le 300-n$。
* $k \in \{0, 1, 2\}$。
* $1 \le u_i \le n+m_1$。
* $1 \le v_i \le n+m_1$。
* $1 \le u_i' \le n+m_2$。
* $1 \le v_i' \le n+m_2$。
* 给定的 $T_1$ 与 $T_2$ 保证连通,且
1. 若 $u \in \{1, 2, \ldots, n\}$,则在 $T_1$ 与 $T_2$ 中 $\deg(u) = 1$。
1. 若 $u \in \{n+1, n+2, \ldots, n+m_1\}$,则在 $T_1$ 中 $\deg(u) \ge 3$。
1. 若 $u \in \{n+1, n+2, \ldots, n+m_2\}$,则在 $T_2$ 中 $\deg(u) \ge 3$。
* 输入的数皆为整数。
### 评分说明
本题共有四组子任务,条件限制如下所示。
每一组可有一或多个测试数据,该组所有测试数据皆需答对才会有该组分数。
| 子任务 | 分数 | 额外输入限制 |
| :------: | :----: | ------------ |
| 1 | $21$ | $k = 0$ |
| 2 | $13$ | $k \in \{0, 1\}$ |
| 3 | $23$ | $n+m_1 \le 30$ 且 $n+m_2 \le 30$ |
| 4 | $43$ | 无额外限制 |