P11905 [NHSPC 2023] D. 共同子凸包
题目描述
在数学上,一个点集合 $S$ 的**凸包** (convex hull) 定义为包含 $S$ 的最小凸集合,记作 $\operatorname{Conv}(S)$。在平面上,若 $S$ 为非空有限点集合,则 $\operatorname{Conv}(S)$ 为一包含内部与边界的最小凸多边形,或其退化形式。另一方面,设 $E_1$ 与 $E_2$ 为平面上的两个点集合。若存在某个二维向量 $\mathbf{v}$,满足
$$P \in E_1 \iff P+\mathbf{v} \in E_2,$$
则称 $E_1$ 与 $E_2$ 经过平移后重合。
现给定平面上的有限点集合 $S_1$ 与 $S_2$,并考虑它们的非空子集合 $T_1\subseteq S_1$ 与 $T_2\subseteq S_2$。已知子凸包 $\operatorname{Conv}(T_1)$ 与子凸包 $\operatorname{Conv}(T_2)$ 面积皆大于 $0$ 且经过平移后重合,请求出 $\operatorname{Conv}(T_1)$ 所有可能的面积。
以下展示两个子凸包平移后重合的例子。
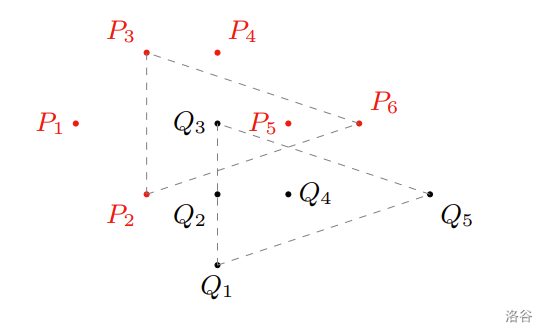
输入格式
> $n$ $m$
> $x_1$ $y_1$
> $x_2$ $y_2$
> $\vdots$
> $x_n$ $y_n$
> $\xi_1$ $\eta_1$
> $\xi_2$ $\eta_2$
> $\vdots$
> $\xi_m$ $\eta_m$
* $n$ 代表 $S_1$ 的集合大小。
* $m$ 代表 $S_2$ 的集合大小。
* $x_i, y_i$ 代表 $S_1$ 包含点 $(x_i, y_i)$。
* $\xi_i, \eta_i$ 代表 $S_2$ 包含点 $(\xi_i, \eta_i)$。
输出格式
> $k$
> $a_1$
> $a_2$
> $\vdots$
> $a_k$
* $k$ 代表若子凸包 $\operatorname{Conv}(T_1)$ 与子凸包 $\operatorname{Conv}(T_2)$ 经过平移后重合,$\operatorname{Conv}(T_1)$ 所有可能的非 $0$ 面积数。
* $a_i$ 为一整数,代表 $\operatorname{Conv}(T_1)$ 所有可能的非 $0$ 面积中,第 $i$ 小的数的**两倍**。
说明/提示
### 测试数据限制
* $3 \le n \le 40$。
* $3 \le m \le 40$。
* $0 \le x_i \le 20$。
* $0 \le y_i \le 20$。
* $0 \le \xi_i \le 20$。
* $0 \le \eta_i \le 20$。
* 对任意 $i, j \in \{1, 2, \ldots, n\}$,若 $i \ne j$,则 $(x_i, y_i) \ne (x_j, y_j)$。
* 对任意 $i, j \in \{1, 2, \ldots, m\}$,若 $i \ne j$,则 $(\xi_i, \eta_i) \ne (\xi_j, \eta_j)$。
* 输入的数皆为整数。
### 评分说明
本题共有四组子任务,条件限制如下所示。
每一组可有一或多个测试数据,该组所有测试数据皆需答对才可获得该组分数。
| 子任务 | 分数 | 额外输入限制 |
| :------: | :----: | ------------ |
| 1 | $7$ | 所有可能的非 $0$ 面积必能从 $T_1$ 与 $T_2$ 中各选 $3$ 个点得到 |
| 2 | $23$ | $n+m \le 30$ |
| 3 | $41$ | $S_1 = S_2$ |
| 4 | $29$ | 无额外限制 |