P11973 [JOI Open 2020] 黑白点 / Monochrome Points
题目描述
在一个环上有 $2n$ 个点,按照顺时针顺序编号为 $1,2,\dots 2n$。每个点是黑点或者白点,一共有 $n$ 个黑点和 $n$ 个白点。
我们画 $n$ 条线段连接环上的点,使其满足以下条件:
- 每个点恰好是一条线段的端点。
- 每条线段连接一个黑点和一个白点。
定义**相交数**为相交的线段对数。
给出每个点的颜色,计算 $n$ 条线段最大的相交数。
输入格式
第一行一个整数 $n$。
第二行一个长度为 $2n$ 的字符串 $S$,第 $i$ 个字符表示第 $i$ 个点的颜色。每个字符是 $\mathtt{B}$(黑色)或 $\mathtt{W}$(白色)。
输出格式
一个数,表示最大的相交数。
说明/提示
#### 样例解释 1
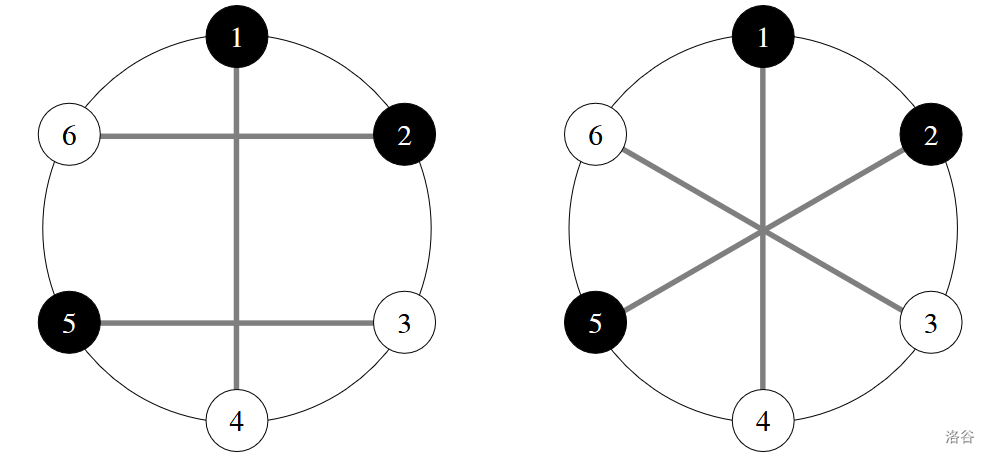
如果我们按左图绘制线段,那么相交数就是 $2$。另一方面,如果我们按右图绘制线段,那么相交数是 $3$,然而不满足题目描述中的条件。
#### 数据规模与约定
#### 本题采用捆绑测试。
- Subtask 1(4 pts):$n\le 8$;
- Subtask 2(21 pts):$n\le 300$;
- Subtask 3(10 pts):$n\le 2000$;
- Subtask 4(65 pts):无特殊限制。
对于 $100\%$ 的数据,$1\le n\le 2\times 10^5$,保证 $S$ 的长度是 $2n$ 且只包含 $\mathtt{B}$ 和 $\mathtt{W}$ 两种字符。保证 $\mathtt{B}$ 和 $\mathtt{W}$ 都出现恰好 $n$ 次。
译自 [JOI Open 2020](https://contests.ioi-jp.org/open-2020/index.html) T2 「[白黒の点](https://s3-ap-northeast-1.amazonaws.com/data.cms.ioi-jp.org/open-2020/monochrome/2020-open-monochrome-statement.pdf) / [Monochrome Points](https://s3-ap-northeast-1.amazonaws.com/data.cms.ioi-jp.org/open-2020/monochrome/2020-open-monochrome-statement-en.pdf)」