P11977 [KTSC 2021] 卡顿 / lag

本题翻译自 [2021년도 국제정보올림피아드 대표학생 선발고사](https://www.ioikorea.or.kr/archives/ioitst/2021/) 1차 선발고사 [#3 렉](https://assets.ioikorea.or.kr/ioitst/2021/1/lag/lag_statement.pdf)。 **请注意，你不需要也不应该实现 `main` 函数。具体实现方式见【实现细节】部分。** **警告：滥用本题评测一次即可封号。**

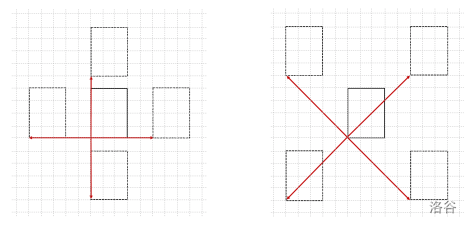
在一台老旧计算机上使用画图程序。画图程序的屏幕是由称为像素的格子组成的网格。 最左下角的像素坐标为 $(1, 1)$，向右第 $a$ 个、向上第 $b$ 个像素的坐标为 $(a, b)$。初始屏幕上画有 $N$ 个具有垂直和水平边的矩形。矩形由该区域内包含的像素表示。 将对 $N$ 个矩形执行 $M$ 个移动命令。矩形的移动方向包括东、西、南、北四个方向，以及东北、西北、东南、西南（与水平轴成 $45$ 度角）四个方向。此外，移动距离 $d$ 也会给定。换句话说，移动命令由方向和距离组成。具体来说，如果矩形的最左下角像素坐标为 $(a, b)$，那么向东、北、西、南方向移动距离 $d$ 后，其左下角坐标将分别变为 $(a + d, b), (a, b + d), (a - d, b), (a, b - d)$。而向东北、西北、西南、东南方向移动距离 $d$ 后，其左下角坐标将分别变为 $(a + d, b + d), (a - d, b + d), (a - d, b - d), (a + d, b - d)$（见图 1）。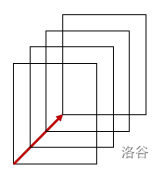  屏幕上矩形 $R$ 的移动距离 $d$ 是通过依次在每移动距离 $1$ 时快速显示 $R$ 的位置来实现的。但由于计算机过于老旧，$R$ 移动时会出现严重的卡顿。因此，$R$ 移动过程中绘制的所有样子都会保留在屏幕上。也就是说，$R$ 移动距离 $d$ 后，屏幕上会新增 $d$ 个矩形。例如，在图 2 中，矩形向东北方向移动距离 $3$ 后，会新增 $3$ 个矩形，最终屏幕上共有 $4$ 个矩形。移动结束后，$R$ 将位于东北方向的终点。  执行完 $M$ 个移动命令后，将给出 $Q$ 个查询。每个查询给出平面上的一个像素 $p$。对于每个查询，需要输出包含像素 $p$ 的矩形数量。 ### 实现细节 你需要实现以下函数： ```cpp vector count_enclosing_rectangle(vector< pair > R1, vector< pair > R2, vector V, vector I, vector D, vector< pair > P ) ``` - 该函数仅被调用一次。 - 参数数组 `R1` 和 `R2` 的大小为 $N$。数组的每个元素表示初始给定的 $N$ 个矩形中的一个，`R1[i]` 和 `R2[i]` 分别表示矩形 $i + 1$ 的最左下角和最右上角像素的坐标。坐标以 $(a, b)$ 的形式给出，表示位置为 $(a, b)$。矩形编号为 $1$ 到 $N$ 的整数。 - 参数数组 `V`、`I`、`D` 的大小为 $M$。数组的每个元素表示 $M$ 个矩形移动中的一个，表示矩形 `I[i]` 向方向 `V[i]` 移动距离 `D[i]`。 - 参数数组 `P` 的大小为 $Q$。数组 `P` 的每个元素表示查询对应的平面上的像素 $p$ 的坐标，以 $(a, b)$ 的形式给出。 - 该函数需要计算每个查询像素 $p$ 被多少个矩形包含，并将结果存储在长度为 $Q$ 的数组中返回。第 $i$ 个值应为第 $i$ 个查询的结果（$0 \leq i \leq Q - 1$）。 提交的源代码中不得调用任何输入输出函数。

示例评测程序按以下格式接收输入： - 第 $1$ 行：$N \ M \ Q$ - 第 $1 + i$ 行（$1 \leq i \leq N$）：$\texttt{R1[i - 1].first R1[i - 1].second R2[i - 1].first R2[i - 1].second}$ - 第 $1 + N + i$ 行（$1 \leq i \leq M$）：$\texttt{V[i - 1] I[i - 1] D[i - 1]}$ - 第 $1 + N + M + i$ 行（$1 \leq i \leq Q$）：$\texttt{P[i - 1].first P[i - 1].second}$

示例评测程序输出以下内容： - 第 $i$ 行（$1 \leq i \leq Q$）：函数 `count_enclosing_rectangle` 返回数组的第 $i$ 个元素。 请注意，示例评测程序与实际评测程序可能不同。

### 约束条件 - $1 \leq N \leq 250,000$ - $0 \leq M \leq 250,000$ - $1 \leq Q \leq 250,000$ - $1 \leq \texttt{R1[i].first} \leq \texttt{R2[i].first} \leq 250,000$ - $1 \leq \texttt{R1[i].second} \leq \texttt{R2[i].second} \leq 250,000$ - $0 \leq \texttt{V[i]} \leq 7$ - $1 \leq \texttt{I[i]} \leq N$ - $1 \leq \texttt{D[i]} \leq 250,000$ - 屏幕上的坐标值在 $1$ 到 $250,000$ 之间。任何矩形包含的所有像素的坐标值始终在此范围内，移动后也满足此条件。查询的像素也满足此条件。 - 矩形移动方向 `V[i]` 的值为：$0$（东）、$1$（东北）、$2$（北）、$3$（西北）、$4$（西）、$5$（西南）、$6$（南）、$7$（东南）。 ### 子任务 1. （$8$ 分） - $N \leq 100$，$M = 0$ 2. （$8$ 分） - $M = 0$ 3. （$11$ 分） - $M \leq 100$ 4. （$13$ 分） - $\text{V}[i] \in \{0, 2, 4, 6\}$（$0 \leq i \leq M - 1$），即矩形仅沿水平或垂直方向移动。 5. （$12$ 分） - $\text{R1}[i] = \text{R2}[i]$（$0 \leq i \leq N - 1$） 6. （$48$ 分） - 无额外约束条件。 ### 评分标准 只有当 `count_enclosing_rectangle` 函数返回的数组长度为 $Q$，并且与正确答案数组的所有元素完全一致时，才判定为该测试用例正确。 ### 示例 - $N = 3$，$M = 3$，$Q = 4$，`R1 = [(1, 1), (3, 3), (4, 1)]`，`R2 = [(2, 2), (4, 4), (6, 2)]`，`V = [1, 6, 2]`，`I = [1, 2, 3]`，`D = [2, 2, 3]`，`P = [(3, 3), (4, 3), (3, 2), (5, 3)]`时，考虑以下情况。 评测程序将调用以下函数： ```cpp count_enclosing_rectangle(R1, R2, V, I, D, P) ``` 在此示例中，$3$ 个矩形的 $3$ 次移动共生成 $7$ 个新矩形，因此最终屏幕上有 $10$ 个矩形。像素 $(3, 3)$ 被矩形 $1$ 生成的 $2$ 个矩形和矩形 $2$ 生成的 $2$ 个矩形包含，因此共被 $4$ 个矩形包含。注意，矩形 $1$ 的第三次移动生成的矩形与矩形 $2$ 的矩形虽然区域相同，但被视为不同的矩形。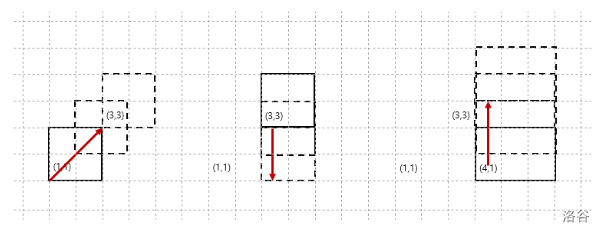  函数 `count_enclosing_rectangle` 应返回数组 `[4, 5, 3, 2]`。