P11981 [KTSC 2021] 猴子 / monkey

本题翻译自 [2021년도 국제정보올림피아드 대표학생 선발고사](https://www.ioikorea.or.kr/archives/ioitst/2021/) 2차 선발고사 [#3 원숭이](https://assets.ioikorea.or.kr/ioitst/2021/2/monkey/monkey_statement.pdf)。 **请注意，你不需要也不应该实现 `main` 函数。具体实现方式见【实现细节】部分。** 提交时，请在程序开头添加如下内容，并且无需引用 `monkey.h`： ```cpp #include #include long long max_bananas(std::vector A, std::vector B, std::vector P); ```

有两根并排的柱子 A 和 B。每根柱子上有 $N$ 个把手，这些把手从下到上依次编号为 $1$ 到 $N$。每根柱子上挂有 $0$ 个或更多香蕉。$A_i$ 表示柱子 A 的第 $i$ 个把手上挂的香蕉数量，$B_j$ 表示柱子 B 的第 $j$ 个把手上挂的香蕉数量。这些值是 $0$ 到 $10^9$ 之间的整数。 猴子可以用双手抓住两根柱子上的不同把手。注意，不能抓住同一根柱子上的两个把手。此外，猴子不能随意抓住任何把手。猴子可以抓住的两个把手的组合可以用 $(x, y)$ 表示，这意味着可以同时抓住柱子 A 的第 $x$ 个把手和柱子 B 的第 $y$ 个把手。此时，猴子可以吃掉这两个把手上剩下的所有香蕉。显然，一旦吃掉香蕉，香蕉就会消失。这样的有序对共有 $M$ 个。 最初，猴子从可以抓住的两个把手的组合中的一个位置出发。当猴子当前位于 $(x, y)$ 时，可以移动到另一个可以抓住的两个把手的组合 $(x', y')$，条件是满足 $x < x'$ 且 $y = y'$，或者 $x = x'$ 且 $y < y'$。 猴子当然希望尽可能多吃香蕉。给定可以抓住的把手的信息以及这些把手上挂的香蕉数量，编写一个程序计算猴子最多可以吃多少香蕉。 ### 实现细节 你需要实现以下函数。 ```cpp long long int max_bananas(vector A, vector B, vector< pair > P) ``` - 此函数仅被调用一次。 - `A` 的长度为 $N$，`A[i]` 表示柱子 A 的第 $i+1$ 个把手上挂的香蕉数量（$0 \leq i \leq N-1$）。 - `B` 的长度为 $N$，`B[i]` 表示柱子 B 的第 $i+1$ 个把手上挂的香蕉数量（$0 \leq i \leq N-1$）。 - `P` 的长度为 $M$，如果 $(x, y)$ 包含在 `P` 中，则猴子可以同时抓住柱子 A 的第 $x$ 个把手和柱子 B 的第 $y$ 个把手，并吃掉这两个把手上剩余的香蕉。保证不会多次给出相同的有序对。 - 此函数应根据输入信息返回猴子最多可以吃的香蕉数量。 在提交的源代码中，任何部分都不得执行输入输出函数。

示例评测程序按以下格式接收输入： - 第 $1$ 行: $N \ M$ - 第 $2$ 行: $A[0] \ A[1] \ \cdots \ A[N - 1]$ - 第 $3$ 行: $B[0] \ B[1] \ \cdots \ B[N - 1]$ - 第 $3 + i$ 行（$1 \leq i \leq M$）: $\texttt{P[i - 1].first P[i - 1].second}$

示例评测程序按以下格式输出： - 第 $1$ 行: 函数 `max_bananas` 返回的值 注意，示例评测程序可能与实际评分器不同。

### 约束条件 - $1 \leq N \leq 500\,000$ - $1 \leq M \leq 500\,000$ - $M \leq N^2$ - $0 \leq A_i \leq 10^9$（$1 \leq i \leq N$） - $0 \leq B_i \leq 10^9$（$1 \leq i \leq N$） - 参数 `P` 给出的有序对 $(x, y)$ 互不相同，且满足 $1 \leq x \leq N$，$1 \leq y \leq N$。 ### 子任务 1. （$11$ 分） - $M \leq 16$ 2. （$42$ 分） - $M \leq 5\,000$ 3. （$97$ 分） - 无额外约束条件。 ### 评分标准 只有当 `max_bananas` 函数返回的香蕉数量与正确答案完全一致时，该测试用例才被视为正确。 注意，每个子任务的得分是该子任务所有测试用例得分的最小值。 ### 示例 - 考虑 $N = 3$，$M = 3$，$A = [2, 3, 1]$，$B = [3, 2, 4]$，$P = [(1, 1), (2, 1), (1, 3)]$ 的情况。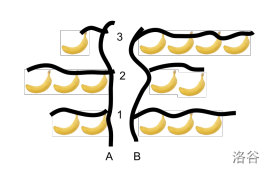  评分器将调用以下函数： ```cpp max_bananas([2, 3, 1], [3, 2, 4], [(1, 1), (2, 1), (1, 3)]) ``` 从 $(1, 1)$ 出发，移动到 $(1, 3)$，总共可以吃掉 $2 + 3 + 4 = 9$ 个香蕉，这是最多可能的香蕉数量。因此，`max_bananas` 函数应返回 $9$。 此示例满足所有子任务的约束。