P12007 【MX-X10-T3】[LSOT-4] National Competition?

> Do you really think we can make it to the national competition?

The wind ensemble club at Kitauji High School (Kyoto Municipal Kitauji High School) has $n$ students numbered from $1$ to $n$. Before Taki Noboru's arrival, $m$ partnership relationships ($0 \le m \le n - 1$) had been established. Each partnership $u, v, w$ indicates that after $u$ or $v$ performs, the other can complete the coordination within $w$ units of time. If two students have no direct partnership, they can still coordinate indirectly through multiple partnerships, with the total error time being the sum of all intermediate coordination times. The current club is as disorganized as a pile of scattered sand! To address this, Taki Noboru has $n - m - 1$ special training plans. The $i$-th plan allows any two members to establish a partnership, achieving coordination in $a_i$ units of time. The **disharmony degree** is defined as the sum of the minimum error times for all pairs $1 \le x < y \le n$. If any pair cannot coordinate in the end, the configuration is considered invalid. To reach the national competition, Taki wants to minimize the disharmony degree. Calculate the optimal disharmony degree for Taki. The data guarantees at least one valid configuration. Since the result might be large, output the disharmony degree modulo $10^9 + 7$.

- The first line contains two integers $n$ and $m$. - The next $m$ lines each contain three integers $u, v, w$, describing a partnership. - If $n - m - 1 > 0$, the last line contains $n - m - 1$ integers $a_1, \ldots, a_{n - m - 1}$.

One line containing an integer—the minimal disharmony degree modulo $10^9 + 7$.

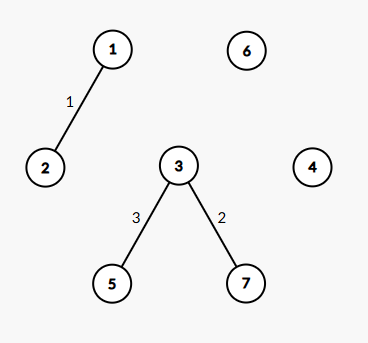
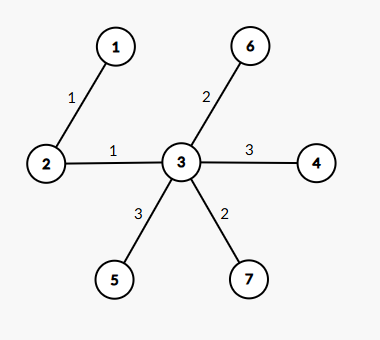
**Sample Explanation #1** The initial partnerships form the structure shown in:  The optimal training adds partnerships as shown in:  For pair $(1,7)$, the minimum error time is $4$, achieved through the path $(1,2) \rightarrow (2,3) \rightarrow (3,7)$. The total sum of all minimum error times is $76$. No better valid configuration exists. **Data Range** **This problem uses subtasks with bundled testing.** - Subtask 1 (13 pts): $n \le 6$. - Subtask 2 (22 pts): $n \le 2000$. - Subtask 3 (18 pts): Before adding new partnerships, any pair of coordinating members can connect via at most one intermediate member. - Subtask 4 (19 pts): $a_i = 0$, $w = 1$. - Subtask 5 (15 pts): All $a_i$ are equal. - Subtask 6 (13 pts): No additional constraints. For all data: $0 \le m < n \le 10^6$, $0 \le a_i, w \le 10^6$, $1 \le u, v \le n$. Translation by DeepSeek R1