P12016 [NOISG 2025 Finals] 震踏

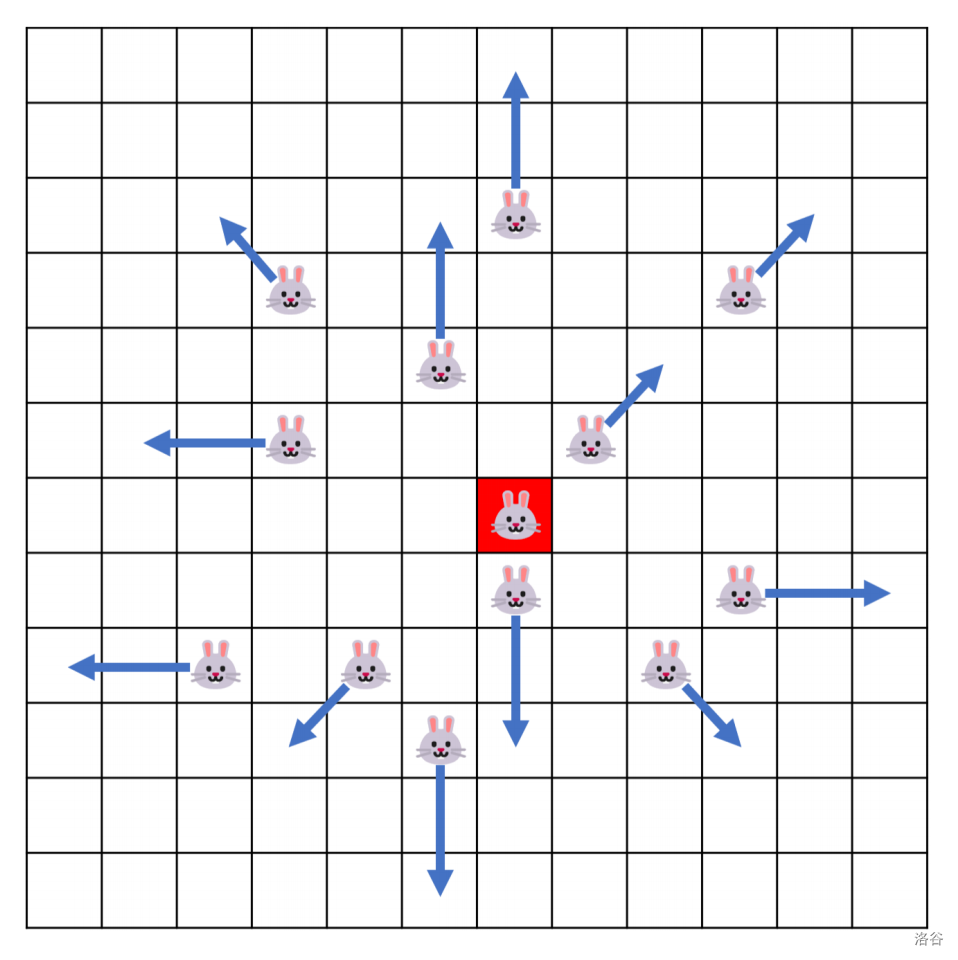
Bunnyland 有广阔的田野，Bunnyland 矮兔（一种本地兔子物种）在其中自由活动。其中一个田野可以建模为一个 $10^9 \times 10^9$ 的网格单元。网格的行从北到南编号为 $1$ 到 $10^9$，网格的列从西到东编号为 $1$ 到 $10^9$。我们将网格中位于第 $r$ 行、第 $c$ 列的单元格称为单元格 $(r, c)$。 在这片田野中，有 $n$ 只兔子，编号从 $1$ 到 $n$。第 $i$ 只兔子最初位于单元格 $(r[i], c[i])$。**最初没有两只兔子位于同一个单元格**。 当兔子感到烦躁时，它们会抬起后腿并踢打地面，这一动作被称为震踏。这 $n$ 只兔子将执行一系列 $m$ 次震踏。在第 $j$ 秒开始时，编号为 $t[j]$ 的兔子会进行震踏。当一只兔子震踏时，所有其他兔子都会远离震踏的兔子。  具体来说，当兔子 A 震踏时，兔子 B 将按照以下方式移动： - 如果 A 和 B 之间的行数小于列数，则 B 将在列方向上远离 A 两列。 - 如果 A 和 B 之间的行数等于列数，则 B 将在列方向和行方向各远离 A 一格。 - 如果 A 和 B 之间的行数大于列数，则 B 将在行方向上远离 A 两行。 可以证明，在震踏发生后，兔子的位置仍然是唯一的。 兔子 Benson 在退休后寻找它的同类，但由于震踏的发生，兔子们四散开来。请帮助 Benson 确定在所有震踏发生后 $n$ 只兔子的最终位置！ 可以保证，在震踏序列过程中，兔子不会离开网格。你也可以假设，兔子在任何情况下都不会移动，除了震踏。

无

无

### 子任务 对于所有测试用例，输入将满足以下约束条件： - $1 \leq n, m \leq 500\,000$ - 对于所有 $1 \leq i \leq n$，有 $1 \leq r[i], c[i] \leq 10^9$ - 对于所有 $1 \leq j \leq m$，有 $1 \leq t[j] \leq n$ - 对于所有 $i \neq j$，有 $(r_i, c_i) \neq (r_j, c_j)$ - 可以保证，在震踏序列过程中，兔子不会离开网格。 你的程序将在满足以下特殊性质的输入数据上进行测试： | 子任务 | 分数 | 特殊性质 | | :-: | :-: | :-: | | $0$ | $0$ | 样例 | | $1$ | $18$ | $n, m \leq 2000$ | | $2$ | $21$ | $r[i] = 1$ | | $3$ | $32$ | $n \leq 2000$ | | $4$ | $13$ | $n \leq 100\,000$ | | $5$ | $16$ | 无 | ### 样例 1 解释 此测试用例适用于子任务 $1, 3, 4, 5$。 兔子 $1$ 处于单元格 $(1, 1)$，兔子 $2$ 处于单元格 $(2, 2)$。 由于兔子 $1$ 和兔子 $2$ 之间的行数等于列数，因此当兔子 $1$ 震踏时，兔子 $2$ 会在东南方向各远离一格，最终到达单元格 $(3, 3)$。震踏的兔子 $1$ 位置保持不变。 ### 样例 2 解释 此样例适用于子任务 $1, 3, 4, 5$。 题目中的图示对应于此测试用例。蓝色箭头显示了当编号为 $1$ 的兔子（位于单元格 $(7, 7)$）震踏时，其他兔子的移动方式。 ### 样例 3 解释 此样例适用于所有子任务。