P12017 [NOISG 2025 Finals] Reachability

Sheepland is a country with $n$ cities. There are $n − 1$ roads connecting pairs of cities with each other. Road $j$ directly connects cities $u[j]$ and $v[j]$. Initially, it is possible to travel from any city to any other city using only these roads. All $n - 1$ roads in Sheepland are planned to be renovated. Under the renovation plan, each road $j$ will be in one of four states: 1. Two-way: citizens from both cities $u[j]$ and $v[j]$ may cross this road into the other city. 2. One-way from city $u[j]$ to city $v[j]$: only citizens from city $u[j]$ may cross this road into city $v[j]$. 3. One-way from city $v[j]$ to city $u[j]$: only citizens from city $v[j]$ may cross this road into city $u[j]$. 4. Closed: no citizens from cities $u[j]$ or $v[j]$ may cross this road into the other city. Unfortunately, the renovation plan has gone missing! To try to recover it, you ask the mayor of each city how many cities are reachable from their city under the renovation plan. The mayor of the $i$-th city replies with $l[i]$. However, some mayors may have provided incorrect values. A city $v$ is considered reachable from a city u if there exists a sequence $c_1, c_2, c_3, \ldots, c_k$ where $c_1 = u, c_k = v$ and a crossable road exists from $c_x$ to $c_{x+1}$ for all $1 \leq x \leq k - 1$. In particular, a city is reachable from itself. Help Sheepland determine whether there exists a renovation plan that is consistent with the number of cities reachable from each city, as reported by all mayors!

Your program must read from standard input. The first line of input contains one integer $n$. The second line of input contains $n$ space-separated integers $l[1], l[2], \ldots, l[n]$. The following $n - 1$ lines of input each contain two space-separated integers. The $j$-th of these lines contains $u[j]$ and $v[j]$.

Your program must print to standard output. Output `YES` if a renovation plan that is consistent with the number of cities reachable from each city, as reported by all mayors, exists and `NO` otherwise.

### Subtasks For all test cases, the input will satisfy the following bounds: - $1 \leq n \leq 5000$ - $1 \leq l[i] \leq n$ for all $1 \leq i \leq n$ - $1 \leq u[j], v[j] \leq n$ for all $1 \leq j \leq n - 1$ - $u[j] \neq v[j]$ for all $1 \leq j \leq n − 1$ - Initially, it is possible to travel from any city to any other city using roads only. Your program will be tested on input instances that satisfy the following restrictions: | Subtask | Marks | Additional Constraints | | :-: | :-: | :-: | | $0$ | $0$ | Sample test cases | | $1$ | $4$ | $n \leq 7$ | | $2$ | $5$ | $n \leq 15$ | | $3$ | $11$ | $l[1] = l[2] = \cdots = l[n]$ | | $4$ | $10$ | If a plan exists, at least one such plan has no two-way roads | | $5$ | $45$ | $n \leq 400$ | | $6$ | $25$ | No additional constraints | ### 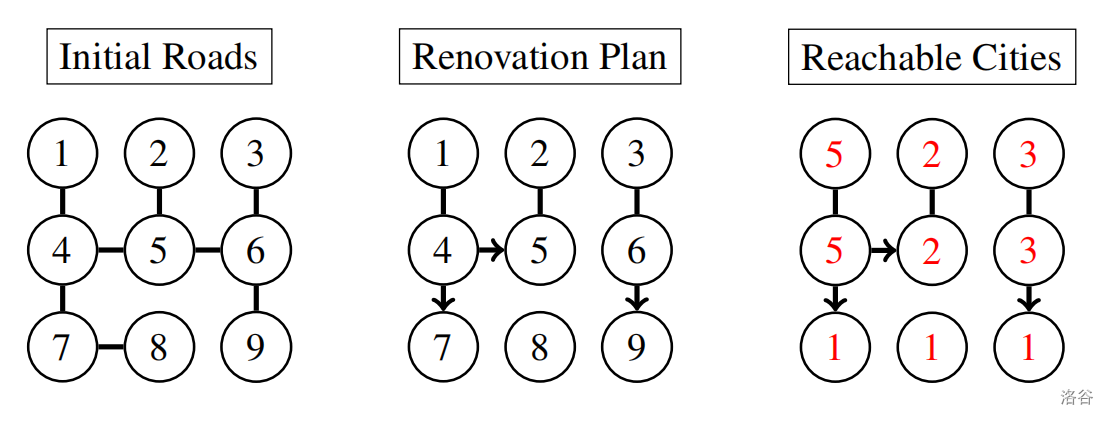Sample Test Case 1 Explanation This test case is valid for subtasks $2, 5$, and $6$. Refer to the diagram below. The renovation plan is consistent with the number of cities reachable from each city, as reported by all mayors.  ### Sample Test Case 2 Explanation This test case is valid for subtasks $2, 4, 5$, and $6$. There does not exist a renovation plan consistent with the number of cities reachable from each city, as reported by all mayors. ### Sample Test Case 3 Explanation This test case is valid for subtasks $1, 2, 5$, and $6$.