P12031 [USACO25OPEN] Forklift Certified P

checker 提供者：kjhhjki

Farmer John is training to become forklift certified! As part of his training, he needs to clear $N$ ($1 \le N \le 10^5$) boxes, conveniently labeled 1 through $N$, from an old warehouse. The boxes can be modeled as axis-aligned rectangles in a 2-dimensional plane, where the $+x$-direction is east and the $+y$-direction is north. Box $i$ has its southwest corner at $(x_{i1}, y_{i1})$ and its northeast corner at $(x_{i2}, y_{i2})$. All coordinates are integers in the range $[1, 2N]$, and no two corners from two different rectangles share the same $x$ or $y$ coordinate. All boxes have a non-zero area, and no two boxes intersect. Farmer John plans to remove the boxes one at a time out of the southwest entrance of the warehouse. However, he can only remove a box if no part of any other box lies both south and west of the box's northeast corner due to physical limitations of the forklift. 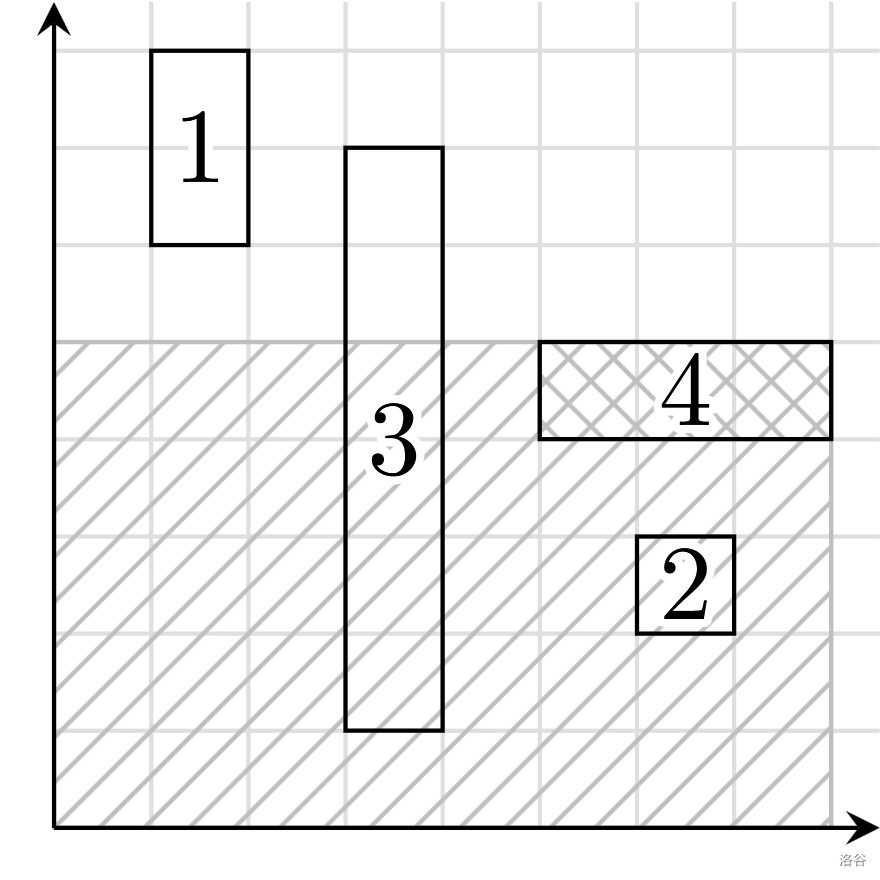An example with $N = 4$ is shown below. To remove box 4, there cannot be any other boxes in the shaded region. Boxes 2 and 3 prevent box 4 from being removed, but box 1 does not.  Help Farmer John decide how to remove all the boxes! Your code should operate in two separate modes, defined by an integer flag $M$: * **Mode 1** ($M = 1$): Generate a permutation of $1, \dots, N$ specifying a valid box removal order. If there are multiple valid orders, find any. It can be proven that such an order always exists. * **Mode 2** ($M = 2$): For each $k = 1, \dots, N$, output 1 if Farmer John can remove box $k$ if boxes $1, \dots, k-1$ have already been removed, and 0 otherwise.

Each input consists of $T$ ($1 \le T \le 10$) independent test cases. It is guaranteed that the sum of all $N$ within each input does not exceed $5 \cdot 10^5$. The first line of input contains $T$ and $M$. (Note that $M$ is the same for each test case.) Each test case is then formatted as follows: * The first line contains a single integer $N$. * Each of the next $N$ lines contains four space-separated integers $x_{i1}, y_{i1}, x_{i2}, y_{i2}$: the locations of the southwest and northeast corners of box $i$.

For each test case: * If $M = 1$, output a single line with $N$ space-separated integers, where the $j$-th integer is the label of the $j$-th box to remove. * If $M = 2$, output a single line with a binary string of $N$ characters specifying the answer for each $k = 1, \dots, N$.

### Sample 1 Explanation The first test case corresponds to the $N = 4$ example above. Box 1 is not blocked by anything, box 3 is blocked by box 1, box 2 is blocked by box 3, and box 4 is blocked by boxes 2 and 3. ### Sample 2 Explanation For the first test case, box 2 is blocked by box 3, so Farmer John cannot remove it before removing box 3. ### Scoring - Inputs 3-5: $M=1$, $N≤1000$. - Input 6: $M=2$, $N≤1000$. - Inputs 7-13: $M=1$, no additional constraints. - Inputs 14-16: $M=2$, no additional constraints.