P12041 [USTCPC 2025] 图上交互题 2 / Constructive Minimum Mex Path

USTCPC 设置 3s 时限为了使得 python 通过。洛谷改为 1s 时限。 2024 年 1 月 13 日 15:59:31，随着最后一发交互 J 题的提交出现了 Wrong Answer，小 G 的 EC-Final 比赛结束了，也意味着在 ICPC 生涯中第一次打铁。 克露丝卡尔酱想要帮助她的同学小 G！她打算批量生产交互题给小 G 做。如何批量生产交互题？只要在一个数据结构中有若干个未知量 $a_i$，每次询问给定向量 $x$，交互库会返回关于 $a_i$ 的函数 $f(x)$，这样就能批量生产交互题了！ ~~为什么题目名里有 2 呢？~~

给定一个 $n$ 个点，$m$ 条边的**无向图**。第 $i$ 条边 $(u_i,v_i)$ 有一个**未知边权** $a_i$。 对于任何一条**路径**，定义其**代价**如下：设路径为 $(p_0,p_1,...,p_k)$，其中要求 $(p_{i-1},p_i)$ 是无向图中的边，设其为第 $e_i$ 条边。那么路径的代价即为 $\mathop{\text{mex}}\limits_{i=1}^{k} a_{e_i}$。（该路径可以经过重复点和重复边，即 $p$ 和 $e$ 可以包含重复的数） $\text{mex}$ 是一种定义域为一个非负整数的可重集合，函数值为非负整数的映射，定义为集合内最小未在集合内出现过的非负整数。 定义 $f(x,y)$ 为从 $x$ 到 $y$ 的所有路径中代价的**最小值**。特别地，当 $x=y$ 时，$f(x,y)=0$。 给定 $n,m$，再对于每条边 $(u_i,v_i)$ 给定 $f(u_i,v_i)$，你需要求出是否存在一组合法的 $a_i$，如果有解，你还需要构造一组解。

第一行两个正整数 $n,m$ $(1\le n,m\le 10^5)$。 第 $2\sim m+1$ 行每行两个正整数 $u_i,v_i$ $(1\le u_i,v_i\le n)$ 和一个非负整数 $f(u_i,v_i)$ $(0\le f(u_i,v_i)

如果不存在解，则仅输出 `No`。 否则，在第一行输出 `Yes`，在第二行输出 $m$ 个非负整数 $a_i$ 表示一组合法的解。 答案可能有很多组，此时输出任意一组解即可。你需要保证 输出的 $0\le a_i

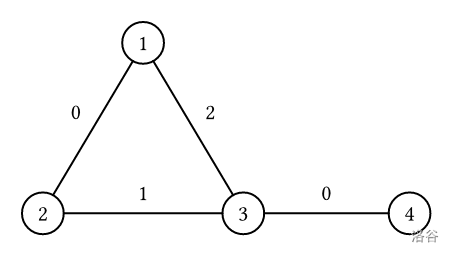
 考虑 $f(1,2)$： + 考虑路径 $1\rightarrow 2$，路径的代价为 $\text{mex}\{0\}=1$。 + 考虑路径 $1\rightarrow 2\rightarrow 3\rightarrow 1\rightarrow 2$，路径的代价为 $\text{mex}\{0,1,2,0\}=3$。 + 考虑路径 $1\rightarrow 3\rightarrow 2$，路径的代价为 $\text{mex}\{1,2\}=0$。 此外还存在其他路径，但可以证明不存在代价比 $0$ 更小的路径，故 $f(1,2)=0$。