P12043 [USTCPC 2025] 图上交互题4 / Constructive Shortest Path

USTCPC 设置 3s 时限为了使得 python 通过。洛谷改为 1s 时限。 2024 年 12 月 28 日 14:59:50，随着最后一发 E 题的提交出现了 Wrong Answer，小 G 的 EC-Final 比赛结束了。 虽然这道铜牌细节题没有通过，但小 G 还是如愿以偿的获得了银牌。为什么呢？他的队友和他合力砍下了一道金牌题 K，这题非常考验对于最短路算法的理解。 克露丝卡尔酱衷心地希望大家能够对于不同的算法有深刻的理解而非仅仅是背诵，因而出了这道题同样也考验对于最短路算法的理解。 ~~小 G 的竞赛生涯还会继续吗？谁知道呢？~~

给定一个 $n$ 个点，$m$ 条边的**无向图**。第 $i$ 条边 $(u_i,v_i)$ 有一个**未知边权** $a_i$。 对于任何一条**路径**，定义其**代价**如下：设路径为 $(p_0,p_1,...,p_k)$，其中要求 $(p_{i-1},p_i)$ 是无向图中的边，设其为第 $e_i$ 条边。那么路径的代价即为 $\sum\limits_{i=1}^{k} a_{e_i}$。（该路径可以经过重复点和重复边，即 $p$ 和 $e$ 可以包含重复的数） 定义 $f(x,y)$ 为从 $x$ 到 $y$ 的所有路径中代价的**最小值**。特别地，当 $x=y$ 时，$f(x,y)=0$。 给定 $n,m$，再对于每条边 $(u_i,v_i)$ 给定 $f(u_i,v_i)$，你需要求出是否存在一组合法的 $a_i$，如果有解，你还需要构造一组解。 注： $f(x,y)$ 就是最短路径的长度，这么写题面只是为了与该系列其它题目风格类似。

第一行两个正整数 $n,m$ $(1\le n\le 500,1\le m\le 10^5)$。请注意本题数据范围 $n$ 的不同。 第 $2\sim m+1$ 行每行两个正整数 $u_i,v_i$ $(1\le u_i,v_i\le n)$ 和一个非负整数 $f(u_i,v_i)$ $(0\le f(u_i,v_i)

如果不存在解，则仅输出 `No`。 否则，在第一行输出 `Yes`，在第二行输出 $m$ 个非负整数 $a_i$ 表示一组合法的解。 答案可能有很多组，此时输出任意一组解即可。你需要保证 输出的 $0\le a_i

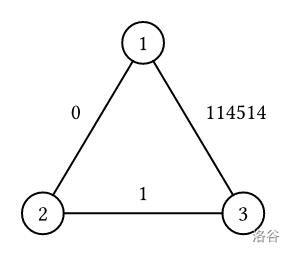
 考虑 $f(3,1)$： + 考虑路径 $3\rightarrow 1$，路径的代价为 $114514$。 + 考虑路径 $3\rightarrow 1\rightarrow 2\rightarrow 3\rightarrow 1$，路径的代价为 $114514+0+1+114514=114515$。 + 考虑路径 $3\rightarrow 2\rightarrow 1$，路径的代价为 $1+0=1$。 此外还存在其他路径，但可以证明不存在代价比 $1$ 更小的路径，故 $f(3,1)=1$。